问题一
问题描述
设计一栈结构,使得出栈、入栈以及求栈的最小值均能在$O (1)$时间内完成
问题分析
针对出入栈,由数据结构的顺序栈知识可以得知,出入栈的时间复杂度都是$O (1)$,因此对于出入栈只需要普通栈就可以实现问题要求;
针对求栈的最小值,使用遍历法求栈最小值的时间复杂度为$O (n)$,因此需要设计一种特殊栈,通过记录栈中的最小值,在求栈的最小值时只需要将最小值输出即可,其时间复杂度为$O (1)$。
算法思路
先构建顺序栈的数据结构
typedef struct{//顺序栈
SElemType* base;
SElemtyoe* top;
int stacksize;
}SqStack;然后构建一个特殊的辅助栈,包括存储所有数据的原栈和存储最小值序列的新栈
typedef struct{//记录最小值的辅助栈
SqStack Data;
Sqstack MinData;
}MinStack;入栈操作
对于第一个元素,一定会进入两个栈;
对于后面的每一元素一定会进入Data栈,如果该元素<=Mindata栈的栈顶元素,则该元素进入Mindata栈,否则不进入
void MinPush(Minstack* minstack, SElemType e) {
Push(&minstack->Data, e);
if (minstack->MinData.base==minstack->MinData.top) {
Push(&minstack->MinData, e);
}
else {
if (e <= GetTop(minstack->MinData)) {
Push(&minstack->MinData, e);
}
}
}出栈操作
对于某一元素的出栈,Data栈一定会执行出栈操作,如果Data栈的栈顶元素和MinData栈的栈顶元素相同,则MinData栈也执行出栈操作
void MinPop(Minstack* minstack, SElemType* e) {
if (GetTop(minstack->Data) == GetTop(minstack->MinData)) {
Pop(&minstack->Data, e);
Pop(&minstack->MinData, e);
return;
}
Pop(&minstack->Data, e);
}求栈最小值
最小值已经存储在MinData栈中,因此只需要获取MinData栈的栈顶元素就可以得到栈的最小值
SElemType GetMin(Minstack* minstack) {
return GetTop(minstack->MinData);
}算法代码与分析
#include<iostream>
#define STACK_INIT_SIZE 100
using namespace std;
typedef int SElemType;
typedef struct {
SElemType* base;
SElemType* top;
int stacksize;
}SqStack;
typedef struct {
SqStack Data;
SqStack MinData;
}Minstack;
void InitStack(SqStack* s) {
s->base = (SElemType*)malloc(STACK_INIT_SIZE * sizeof(SElemType));
s->top = s->base;
s->stacksize = STACK_INIT_SIZE;
}
void Push(SqStack* s, SElemType e) {
if (s->top - s->base >= s->stacksize) {
s->base = (SElemType*)realloc(s->base, (s->stacksize + 10) * sizeof(SElemType));
s->top = s->base + s->stacksize;
s->stacksize += 10;
}
*s->top++ = e;
}
void Pop(SqStack* s, SElemType* e) {
*e = *--s->top;
}
SElemType GetTop(SqStack s) {
return *(--s.top);
}
void DestroyStack(SqStack* s) {
free(s->base);
s->base = NULL;
s->top = NULL;
s->stacksize = 0;
}
void MinInit(Minstack* minstack) {
InitStack(&(minstack->Data));
InitStack(&(minstack->MinData));
}
void MinDestroy(Minstack* minstack) {
DestroyStack(&minstack->Data);
DestroyStack(&minstack->MinData);
}
void MinPush(Minstack* minstack, SElemType e) {
Push(&minstack->Data, e);
if (minstack->MinData.base==minstack->MinData.top) {
Push(&minstack->MinData, e);
}
else {
if (e <= GetTop(minstack->MinData)) {
Push(&minstack->MinData, e);
}
}
}
void MinPop(Minstack* minstack, SElemType* e) {
if (GetTop(minstack->Data) == GetTop(minstack->MinData)) {
Pop(&minstack->Data, e);
Pop(&minstack->MinData, e);
return;
}
Pop(&minstack->Data, e);
}
SElemType GetMin(Minstack* minstack) {
return GetTop(minstack->MinData);
}
int main() {
Minstack minstack;
SElemType e;
MinInit(&minstack);
MinPush(&minstack, 1);
MinPush(&minstack, 2);
MinPush(&minstack, 3);
MinPush(&minstack, 1);
MinPop(&minstack, &e);
cout << GetMin(&minstack) << endl;
system("pause");
return 0;
}实验结果:
分析:
本算法能够实现出入栈、求栈最小值时间复杂度$O (1)$,但是在数据类型的定义上,关于栈和特殊栈存在重复,经查阅资料,可以采用结构体继承解决。
问题二
问题描述
改进冒泡排序使得在最好情况下可以在线性时间内完成
问题分析
对于普通的冒泡排序算法,在最坏的情况下其时间复杂度为$O (n^2)$。第一趟排序进行了$(n-1)$次比较,第i趟排序进行了$(n-i)$次比较;但是对于$(n-1)$趟排序,如果序列在某一次排序时恰好有序,则在该次之后的每一次排序都是无用的,为了优化冒泡排序,只需要在该次以后终止冒泡排序。
算法思路
设置一个标志变量确定某一序列中的数据是否发生了交换,如果某一次冒泡过程中发现没有交换操作时,则说明序列已经排好序了,终止冒泡排序。
算法代码及分析
#include<iostream>
using namespace std;
void BubbleSort(int array[], int n,int* num) {
for (int i = 0; i < n - 1; i++) {
bool flag = true;
for (int j = 0; j < n - i - 1; j++) {
if (array[j] > array[j + 1]) {
int temp = array[j];
array[j] = array[j + 1];
array[j + 1] = temp;
flag = false;
}
}
if (flag) {
break;
}
(*num)++;
}
}
int main() {
int num = 0;
int array[] = { 5,4,3,6,7,8 };
int n1 = sizeof(array) / sizeof(int);
cout << "排序前:";
for (int i = 0; i < n1; i++) {
cout << array[i] << ",";
}
cout << endl;
BubbleSort(array, n1, &num);
cout << "排序后:";
for (int i = 0; i < n1; i++) {
cout << array[i] << ",";
}
cout << endl;
int array1[] = { 1,2,3,4,5,6 };
int n2 = sizeof(array1) / sizeof(int);
cout << "排序前:";
for (int i = 0; i < n2; i++) {
cout << array1[i] << ",";
}
cout << endl;
cout << num << endl;
num = 0;
BubbleSort(array1, n2, &num);
cout << "排序后:";
for (int i = 0; i < n2; i++) {
cout << array1[i] << ",";
}
cout << endl;
cout << num << endl;
system("pause");
return 0;
}实验结果:
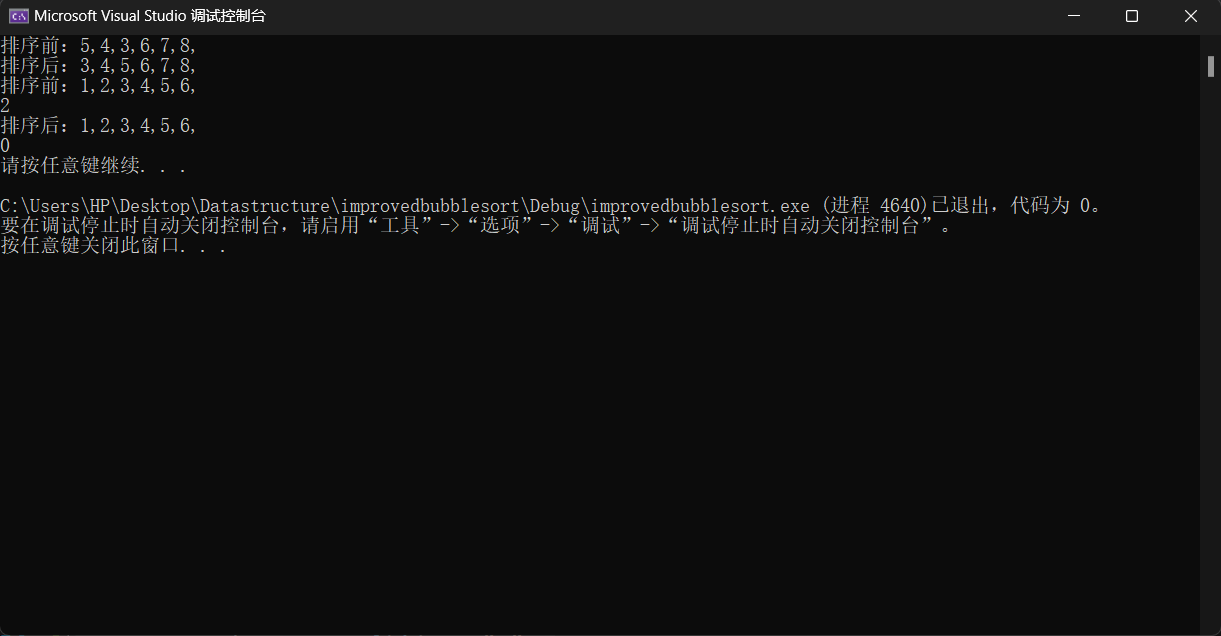
分析:
通过实验分析,在数据极端良好的情况下,能够实现时间复杂度为$O (1)$;在数据较为不良的情况下,仍能减少数据排序次数,使其在线性时间内完成。



