问题一
问题描述
给出策略列举出包含n元素的集合的所有子集,并进行分析
问题分析
通过数学知识,得到子集的个数是$2^n$,而$n$位的二进制码正好可以表示$2^n$个整数,因此可以对每一子集进行二进制编码(其中,第$i$位编码为1则有该元素,为0则没有),使用二进制数所表示的整数来代表每一个子集。
算法思路
使用一字符数组存储包含n个元素的集合$0,1,\cdots,2^n-1$逐一遍历
对数$i$移位操作按位与判断是否存在某一元素
打印输出每一个子集
算法实现与分析
#include<iostream>
using namespace std;
void PrintSet(int array[],int n) {
int m = 1 << n;
for (int i = 0; i < m; i++) {
cout << "{ ";
for (int j = 0; j < n; j++) {
if ((i >> j) & 1) {
cout << array[j] << " ";
}
}
cout << "}" << endl;
}
}
int main() {
int array1[] = { 1,2,3,4 };
int n1 = sizeof(array1) / sizeof(array1[0]);
PrintSet(array1,n1);
cout << endl;
int array2[] = { 1,2,3 };
int n2 = sizeof(array2) / sizeof(array2[0]);
PrintSet(array2, n2);
system("pause");
return 0;
}输出结果:
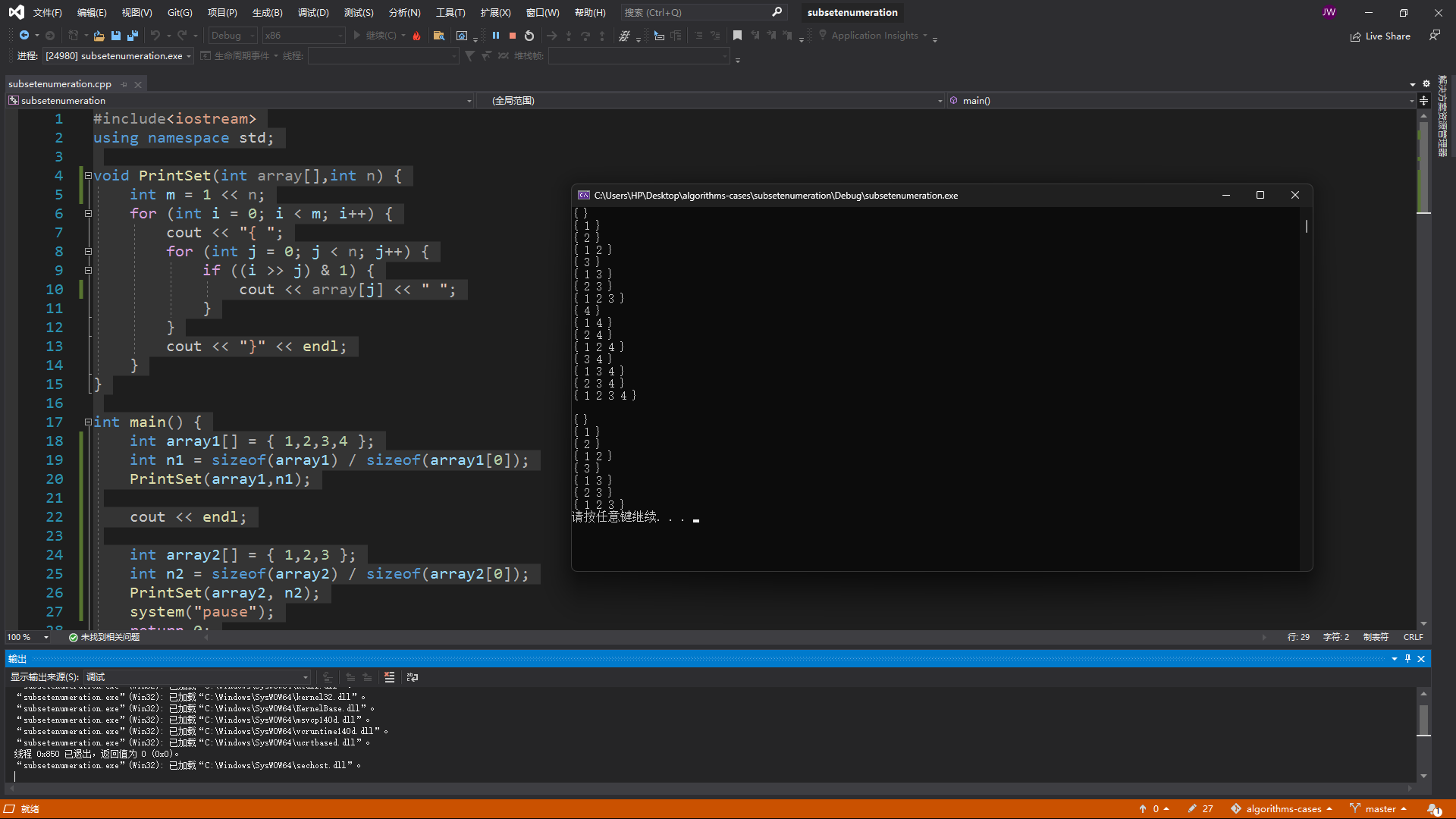
本算法的时间复杂度是$\Omicron(n*2^n)$,对于元素个数大的集合来说,耗费时间相当大
问题二
问题分析
在机器学习、文本处理、推荐系统等应用领域,经常使用相似度指标,调研学习当前业界经常使用的相似度指标
问题关键字
相似度指标
调研学习报告
相似度指标的定义是衡量对象之间的相似程度的数值,相似度指标可以氛围两大类:基于距离和基于角度。
基于距离的相似度指标:
根据两个对象之间的距离来计算相似度,距离越近,相似度越高
常见的指标有欧氏距离、曼哈顿距离、闵可夫斯基距离等
基于角度的相似度指标:
根据两个对象之间的夹角来计算相似度,夹角越小,相似度越高
常见的指标有余弦相似度、皮尔逊相关系数等
常见的相似度指标:
欧几里得距离
根据勾股定理计算两个点之间的直线距离
欧氏距离越小,表示两个对象越相似
公式
$$
\sqrt{\sum_{i=1}^n\left(x_i-y_i\right)^2}
$$
标准化公式
$$
\sqrt{\sum_{k=1}^n\left(\frac{x_{1 k}-x_{2 k}}{s_k}\right)^2}
$$
适用场景
欧氏距离适用于连续变量,比如坐标、长度、速度等
余弦相似度
余弦相似度通过计算两个向量之间的夹角余弦值来衡量它们的方向是否一致
余弦相似度越大,两个对象越相似;值为负,两向量负相关
公式
$$
\cos (\theta)=\frac{\sum_{k=1}^n x_{1 k} x_{2 k}}{\sqrt{\sum_{k=1}^n x_{1 k}^2} \sqrt{\sum_{k=1}^n x_{2 k}^2}}
$$
余弦相似度无法衡量每个维数值的差异,因此引入调整余弦相似度(虽然没有看懂):
调整余弦相似度公式
$$
\operatorname{sim}(i, j)=\frac{\sum_{u \in U}\left(R_{u, i}-\bar{R}u\right)\left(R{u, j}-\bar{R_u}\right)}{\sqrt{\sum_{u \in U}\left(R_{u, i}-\bar{R}u\right)^2} \sqrt{\sum{u \in U}\left(R_{u,j}-\bar{R}_u\right)^2}}
$$
适用场景
余弦相似度适用于稀疏向量,比如文本、图像、音频等
皮尔逊相关系数
在概率论与数理统计中学习到的衡量两变量之间线性相关程度的统计指标
皮尔逊相关系数越接近1或者-1,表示两者越相关
公式
$$
\rho_{X, Y}=\frac{\operatorname{cov}(X, Y)}{\sigma_X \sigma_Y}=\frac{E\left(\left(X-\mu_X\right)\left(Y-\mu_Y\right)\right)}{\sigma_X \sigma_Y}=\frac{E(X Y)-E(X) E(Y)}{\sqrt{E\left(X^2\right)-E^2(X)} \sqrt{E\left(Y^2\right)-E^2(Y)}}
$$
适用场景
皮尔逊相关系数适用于评分数据,比如用户对商品、电影的评分
杰卡德相似系数
一种衡量集合之间重合程度的指标,通过两个集合交集和并集的比值得到
杰卡德相似系数越接近1,表示两个对象越相似
公式
$$
\operatorname{Jaccard}(X, Y)=\frac{X \cap Y}{X \cup Y}
$$
适用场景
杰卡德相似系数适用于二元变量或者名义变量,比如词汇、元素、特征
具体应用
- 在文本处理中,比较两文本之间的语义相似性,可以使用深度学习模型来学习文本向量,适用余弦相似度或其他自定义损失函数来计算文本间的语义匹配程度
- 在推荐系统中,比较用户或者物品之间的偏好或者兴趣,可以使用用户-物品偏好矩阵作为输入数据,并使用欧氏距离或者皮尔逊相关系数等方法来计算用户或者物品之间的协同过滤得分。



