算法课外思考题四

算法查找效率旋转数组

思考题

发布日期: 2023-07-06

文章字数: 1.4k

阅读时长: 5 分

问题一

问题描述

对于一个序列可以采用二分查找或顺序查找，请结合实施查找的次数，确定在什么情况下使用二分查找效率更高？

问题分析

顺序查找是按照序列原有顺序对数组进行遍历比较查询的基本查找算法，时间复杂度是$O(n)$，在最坏的情况下，查询值在数组末尾或没有该查询值，需要遍历完整个数组；

二分查找是在顺序存储结构、元素有序排列中，从表中间开始查找，若不相等，则将表分成前后两个字表，根据中间元素的查询结果在对应表中进行第二次查找，时间复杂度是$O(log_2n)$，在最坏的情况下，没有该查询值，则至少需要查询$\lfloor log_2n \rfloor$次；查询成功时，最多查询$\lceil log_2n \rceil$次。

本题通过记录查找次数来进行比较

算法实现与分析

#include<iostream>
#include<vector>
using namespace std;

//顺序查找
int SequentialSearch(vector<int>& arr, int target) {
	int n = arr.size();
	int num = 0;
	for (int i = 0; i < n; i++) {
		num++;
		if (arr[i] == target) {
			cout << "Search for " << num << " times" << endl;
			return i;
		}
	}
	cout << "Search for " << num << " times" << endl;
	return -1;
}

//二分查找
int BinarySearch(vector<int>& arr, int target) {
	int n = arr.size();
	int left = 0, right = n - 1, middle;
	int num = 0;
	while (left <= right) {
		num++;
		middle = left + ((right - left) >> 2);
		if (arr[middle] == target) {
			cout << "Search for " << num << " times" << endl;
			return middle;
		}
		else if (arr[middle] < target) {
			left = middle + 1;
		}
		else {
			right = middle - 1;
		}
	}
	cout << "Search for " << num << " times" << endl;
	return -1;
}

int main() {
	vector<int> arr = { 1,2,3,4,5,6,7,8,9,10 };
	int target = 7;
	int a = SequentialSearch(arr, target);
	cout << a << endl;
	int b = BinarySearch(arr, target);
	cout << b << endl;

	return 0;
}

实验结果：

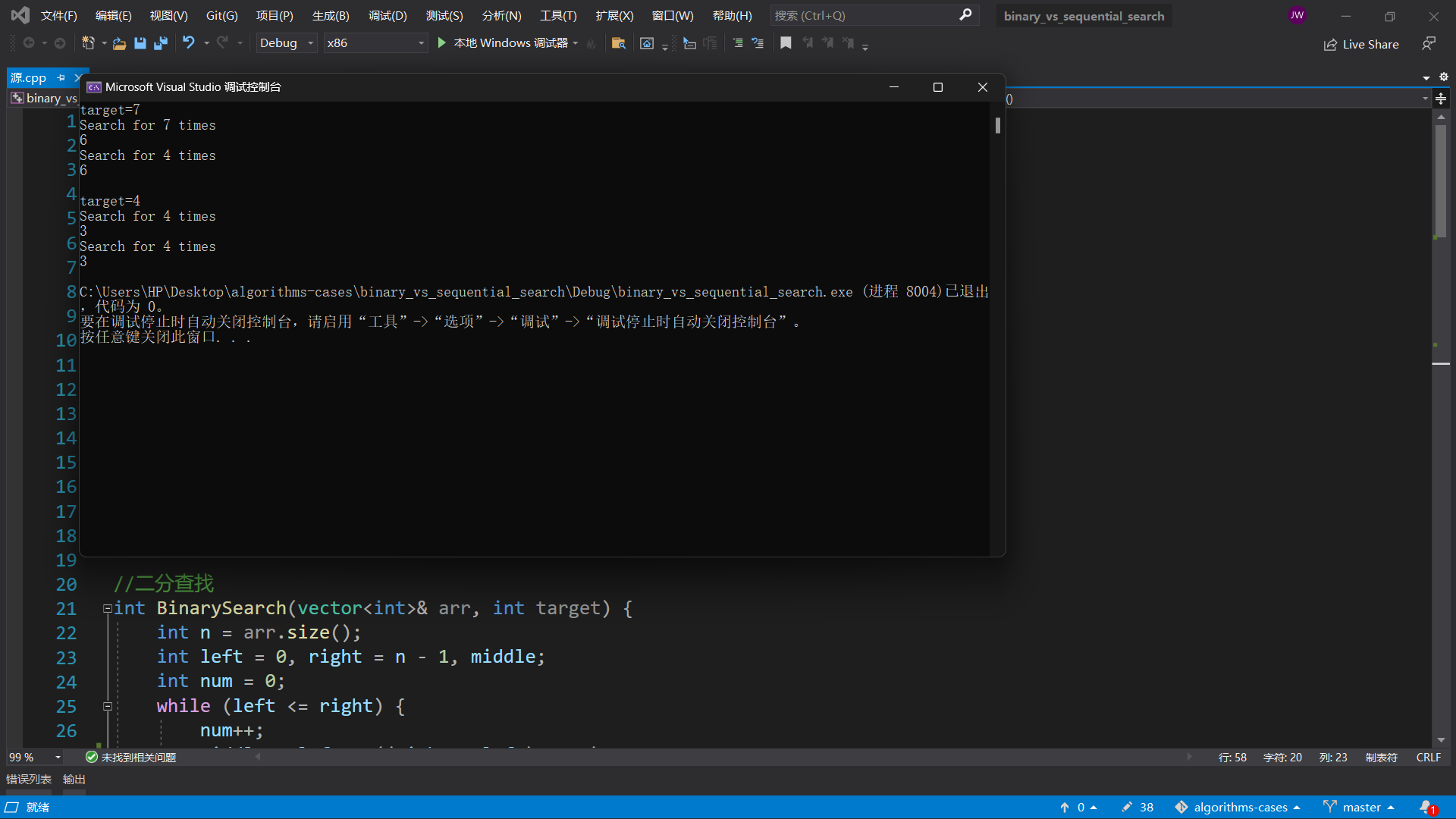
从上述实验中，查询元素7的值，顺序查找的次数为7次，而二分查找的次数为4次，最终查询结果都正确，但是在本序列中，元素数量并不是很多，因此查询次数在数量级上并没有显著差距。

下面对两查找效率进行比较：

以升序序列为例，在最小值片进行查询的时候，顺序查找的次数会小于二分查找，因此使用顺序查找查询较小的值即查询值下标$< \lfloor log_2n \rfloor$时，效率更高、次数更小；
对于升序序列，在查询相对较大的值的时候，二分查找的次数就会小于顺序查找，因此使用二分查找查询较大的值即查询值下标$> \lfloor log_2n \rfloor$，效率更高、次数更少；
对于查询值个数不止一个的操作来说，使用二分查找的效率比顺序查找要高得多，二分查找只需要在初始状态进行一次排序，之后的每次查找都可以利用有序性，而顺序查找则需要每次查询都进行一次数组遍历。

问题二

问题描述

现有一个序列，它是由一个有序系列绕着某个元素旋转得到的。请给出一个在此序列实施查找的有效算法，并对你的算法进行分析

问题分析

有序序列绕着某个元素旋转得到旋转数组可以使用改进后的二分查找进行查询，在循环中进行有序性判断

如果左端元素小于中间元素，则左半部分为有序数组，如果目标值在左半部分，则继续在左半部分进行查找，否则在右半部分查找；若左端元素大于中间元素，那么右半部分为有序数组，若目标值在右半部分，则继续在右半部分进行查找，否则在左半部分进行查找。

另一种办法就是将旋转序列恢复后在进行二分查找，但是恢复旋转序列存在很多问题，一是旋转序列恢复的时间复杂度是$O(n)$，恢复后排序增加操作时间；二是查找得到的值并不是旋转序列的下标，在实际应用中不会使用。

使用顺序查找的办法，时间复杂度是$O(n)$，简单易懂，但是需要遍历整个序列，大规模数据呈现劣势

算法实现与分析

#include<iostream>
#include<vector>
using namespace std;

int BinarySearch(vector<int>& arr, int target) {
	int left = 0, right = arr.size() - 1;
	while (left <= right) {
		int middle = left + ((right - left) >> 1);
		if (arr[middle] == target) {
			return middle;
		}
		if (arr[left] <= arr[middle]) {
			if (target >= arr[left] && target < arr[middle]) {
				right = middle - 1;
			}
			else {
				left = middle + 1;
			}
		}
		else {
			if (target > arr[middle] && target <= arr[right]) {
				left = middle + 1;
			}
			else {
				right = middle - 1;
			}
		}
	}
	return -1;
}

int main() {
	vector<int> arr = { 4,5,6,7,1,2,3 };
	int target = 1;
	cout << BinarySearch(arr, target) << endl;
}