问题一
问题描述
调研学习并给出矩阵的LU分解方法
矩阵的LU分解方法
Doolittle分解
概念
数值分析中得到:
设A为$n*n$阶矩阵,如果A的顺序主子式$A_i$满足$det(A_i)\neq 0(i=1,2,…,n-1)$,则A可分解为一个单位下三角矩阵L与一个上三角矩阵U的乘积,即A=LU,且分解是唯一的
即
$$
\left(\begin{array}{cccc}
a_{11} & a_{12} & \cdots & a_{1 n} \
a_{21} & a_{22} & \cdots & a_{2 n} \
\vdots & \vdots & \ddots & \vdots \
a_{n 1} & a_{n 2} & \cdots & a_{n n}
\end{array}\right)=\left(\begin{array}{cccc}
1 & & & \
l_{21} & 1 & & \
\vdots & \vdots & \ddots & \
l_{n 1} & l_{n 2} & \cdots & 1
\end{array}\right)\left(\begin{array}{cccc}
u_{11} & u_{12} & \cdots & u_{1 n} \
& u_{22} & \cdots & u_{2 n} \
& & \ddots & \vdots \
& & & u_{n n}
\end{array}\right)
$$
由矩阵乘法可以得到u、l关系:
$$
\left{\begin{array}{l}
\boldsymbol{u}{i j}=\boldsymbol{a}{i j}-\sum_{k=1}^{i-1} \boldsymbol{l}{i k} \boldsymbol{u}{k j} \quad j=\boldsymbol{i}: \boldsymbol{n} \
\boldsymbol{l}{i j}=\left(\boldsymbol{a}{i j}-\sum_{k=1}^{j-1} \boldsymbol{l}{i k} \boldsymbol{u}{k j}\right) / \boldsymbol{u}{j j} \quad \boldsymbol{i}=\boldsymbol{j}+\mathbf{1}: \boldsymbol{n}
\end{array}\right.
$$
在计算机运算程序中,可以将两个三角矩阵按照紧凑格式存放在同一个矩阵中,节省存储空间(注意:主对角线上存储的是U矩阵上主对角线的元素,而L矩阵主对角线元素都为1,只要在运算中体现即可):
$$
\left(\begin{array}{cccc}
\boldsymbol{u}{11} & \boldsymbol{u}{12} & \ldots & \boldsymbol{u}{1 n} \
\boldsymbol{l}{21} & \boldsymbol{u}{22} & \cdots & \boldsymbol{u}{2 n} \
\vdots & \vdots & \ddots & \vdots \
\boldsymbol{l}{n 1} & \boldsymbol{l}{n 2} & \cdots & \boldsymbol{u}{n n}
\end{array}\right)
$$
Doolittle分解算法实现
void Doolittle(double** a,int n,double** res){
for (int k = 1; k < n + 1; k++)
{
for (int j = k, i = k + 1; j < n + 1, i < n + 1; j++, i++)
{
double sum_1 = 0;
for (int t = 1; t < k; t++)
{
sum_1 += res[k - 1][t - 1] * res[t - 1][j - 1];
}
res[k - 1][j - 1] = a[k - 1][j - 1] - sum_1;
double sum_2 = 0;
for (int t = 1; t < k; t++)
{
sum_2 += res[i - 1][t - 1] * res[t - 1][k - 1];
}
res[i - 1][k - 1] = (a[i - 1][k - 1] - sum_2) / res[k - 1][k - 1];
}
double sum_1 = 0;
for (int t = 1; t < k; t++)
{
sum_1 += res[k - 1][t - 1] * res[t - 1][n - 1];
}
res[k - 1][n - 1] = a[k - 1][n - 1] - sum_1;
}
}Crout分解
概念
与Doolittle分解类似的,将单位下三角矩阵L与一个上三角矩阵U的乘积替换成下三角矩阵L与一个单位上三角矩阵U的乘积,其实质上,是将U进一步分解为:
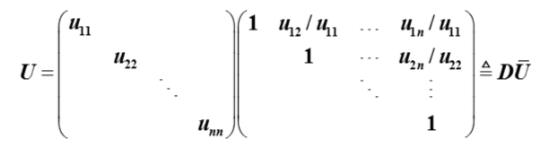
也被称为$LDL^T$分解
Crout分解算法实现
void Cout(double** a,int n,double** res){
for(int k=0;k<n;k++)
{
//同时计算L的第1到K列元素
for(int i=k;i<n;i++)
{
res[i][k]=a[i][k];
for(int j=0;j<=k-1;j++)
res[i][k]-=(res[i][j]*res[j][k]);
}
//同时计算U的第1到K行元素
for(int j=k+1;j<n;j++)
{
res[k][j]=a[k][j];
for(int i=0;i<=k-1;i++)
res[k][j]-=(res[k][i]*res[i][j]);
res[k][j]/=res[k][k];
}
}
}问题二
问题描述
给出方案计算可逆矩阵的逆
问题解决
方法一:Gauss-Jordan消元法
构造一个n*2n的增广矩阵$(A,I_n)$
然后使用高斯消元法,将增广矩阵的左半部分化为单位矩阵,得到的增广矩阵右半部分即为$(I_n,A^{-1})$
高斯消元法:
- 对于一个矩阵A,我们从第1行到第n行不断选取第i列不为0的行,然后做一个行变换(交换两行,使得当前的第i行的第i列不为0)
- 然后将当前的第i行做一个初等变换,也就是都除以$A[i][i]$这样的话就能让第i行第i列变为1
- 将第i行下面的所有行的第i列全部消掉,此时就构成了一个上三角矩阵
- 此时已经构成了一个阶梯型矩阵,我们再从下往上不断将上半矩阵同理消掉即可
算法:
void gauss(){
for(ll i = 1;i <= n; ++i) {//枚举当前处理到第几列
for(ll j = i;j <= n; ++j) {//找到一个第i列不为空的行
if(fabs(a[i][i]) > EPS) {
for(ll k = i;k <= n; ++k) //交换i,j行
swap(a[i][k],a[j][k]);
break;
}
}
if(fabs(a[i][i]) < EPS) {
cout<<"不存在逆矩阵"<<endl;
return ;
}
//这里就是将第i行下面所有行的第i列清空,变成一个阶梯型的矩阵
double aii_inv = 1.0/a[i][i];
//将第i行都乘上a[i][i]的逆
a[i][i] = 1.0;
for(ll j = i + 1;j <= n ; ++j) {
a[i][j] = a[i][j] * aii_inv;
}
for(ll j = 1;j <= n; ++j) {
b[i][j] = b[i][j] * aii_inv;
}
//将第i行下面的所有第i列的元素值清空
for(ll j = i + 1;j <= n; ++j) {
for(ll k = i + 1;k <= n; ++k) {
a[j][k] = a[j][k] - a[i][k] * a[j][i];
}
for(ll k = 1;k <= n; ++k) {
b[j][k] = b[j][k] - b[i][k] * a[j][i];
}
a[j][i] = 0.0;
}
}
}演示:
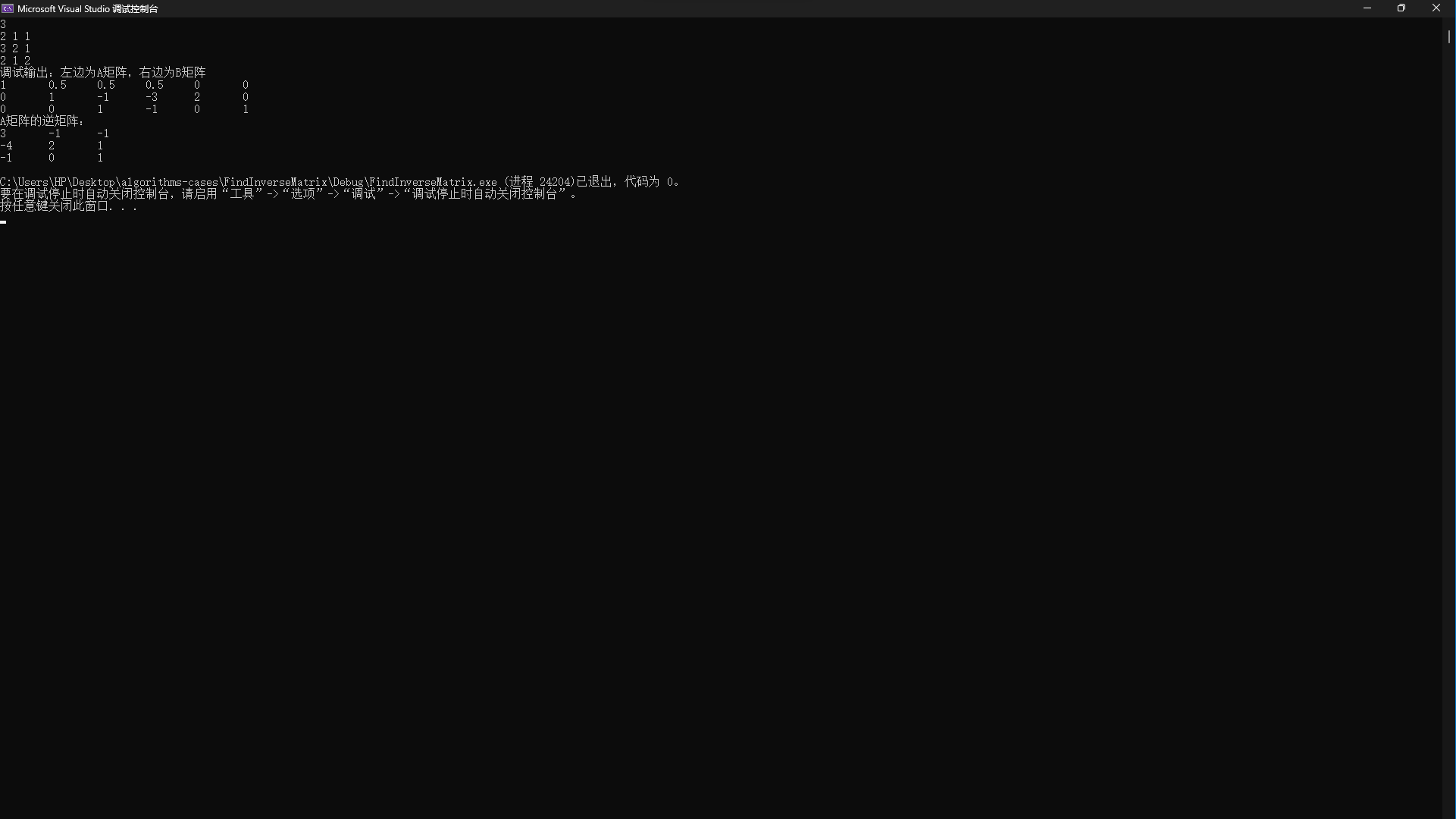
方法二:LU分解法
LU分解法是高斯消元法的一种变种算法,根据上述定义,将矩阵A分解成一个下三角矩阵与一个上三角矩阵:
$$
A=LU
\
A^{-1}=U^{-1}L^{-1}
$$
方法三:SVD分解法
奇异值分解,将矩阵A分解为三个矩阵的乘积分别为:正交矩阵U、对角矩阵W、另一正交矩阵V的转置**$V^T$**
$$
A=UWV^T
\
A^{-1}=VW^{-1}U^T
$$



