算法课外思考题十三

问题一

问题描述

W先生每天驾车去公司上班。W先生的住所位于A，公司位于F，图中的直线段代表公路，交叉点代表路口，直线段上的数字代表两路口之间的平均行驶时间。现在W先生的问题是要确定一条最省时的上班路线。

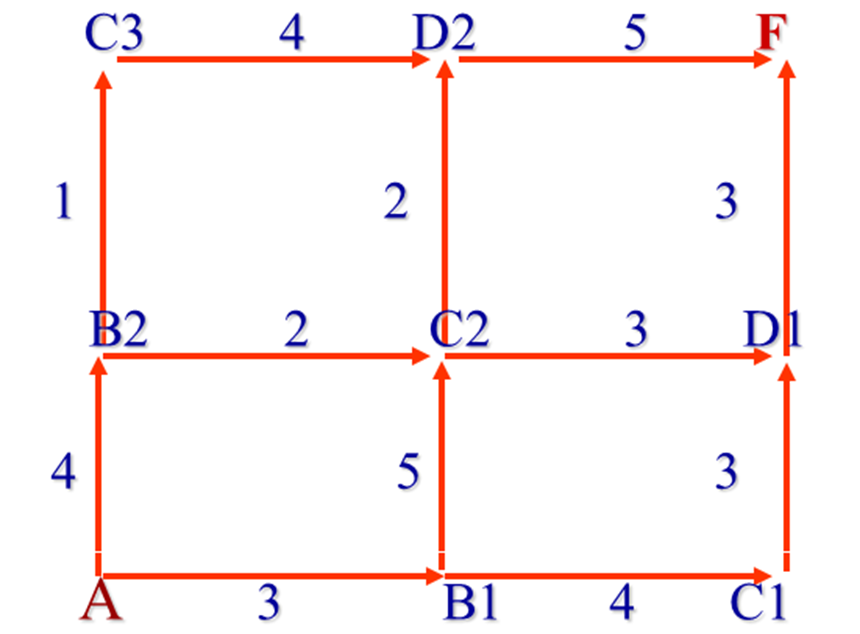
问题分析

这道题目需要计算的是两点之间的最短路径，可以采用两种思想，一种是贪心的思想，另一种就是动态规划的思想，就两种思想展开，阐述具体方法

算法设计

贪心算法（Dijkstra算法）

算法描述

通过迪杰斯特拉算法求最短路径的方法确定上班路线。迪杰斯特拉算法的一般步骤是：

算法求单个源点到其余各顶点的最短路径，计算思路是离源点最低路径长度的开序，运用到的思想是贪心（每次取离源点最近的点）。设C数组为蓝点集，起点为红点。当红点集合加入值时，关联的蓝点将更新最短路径。

我们通过在更新最短路径时对路径经过的点进行记录，可以得到最后的上班路线。

算法实现

#include<iostream>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 510;

struct graph
{
	int n, m;
	int g[N][N];
};

void dijkstra(struct graph &graph)
{
	bool st[N] = { 0 };
	int path[N] = { 0 }, res[N] = { 0 }, dist[N] = { 0 };
	memset(dist, 0x3f, sizeof dist);
	dist[1] = 0;	//初始化
	for (int i = 0; i < graph.n; i++)
	{
		int t = -1;			//t为-1表示还未选择一个点
		for (int j = 1; j <= graph.n; j++)
		{
			if (!st[j] && (t == -1 || dist[t] > dist[j]))
				t = j;		//选取还未被选择的且距离最近的点
		}
		st[t] = true;
		for (int j = 1; j <= graph.n; j++)
		{
			if (dist[j] > dist[t] + graph.g[t][j])
			{
				dist[j] = min(dist[j], dist[t] + graph.g[t][j]);
				path[j] = t;
			}
		}
	}

	cout << "需要的时间最短为:" << dist[graph.n] << endl << "路径依次是:";

	int j = graph.n, i = 0;
	res[i] = graph.n;		// 记录终点
	while (path[j] != 0)	// 将路径存放到结果数组中
	{
		res[++i] = path[j];
		j = path[j];
	}
	for (int m = i; m >= 0; m--)	// 逆序输出
	{
		cout << res[m] << " ";
	}
}

int main()
{
	struct graph graph;
	cin >> graph.n >> graph.m;
	memset(graph.g, 0x3f, sizeof graph.g);
	while (graph.m--)
	{
		int a, b, c;
		cin >> a >> b >> c;
		graph.g[a][b] = min(graph.g[a][b], c);
	}
	dijkstra(graph);
	return 0;
}

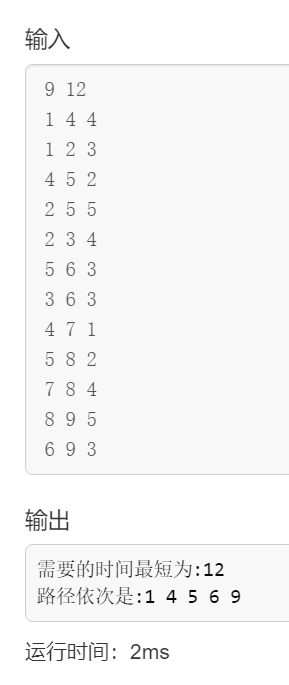
实现结果：

算法的时间复杂度是$O(n^2)$

动态规划算法

算法思路

通过观察发现每个数都是由其左边/下面的数的最短路径和其左边/下面的数到该数的距离的加和得到。我们可以采用动态规划思想，从上到下、从左到右遍历各点，当遍历到最后一个点时，即得需要的最短时间。每次更新最短距离时，可以记录路径，从而确定上班路线。

设置状态函数$dist[i]$，得到公式
$$
dist[i]=min \lbrace dist[i-1]+g[i-1][i],dist[i-m]+g[i-m][i] \rbrace
$$
$dist[i-m]$表示起点到该数下一行数的最短路径

算法实现

#include<iostream>
#include<cstring>
#include<utility>
using namespace std;

const int N = 20;

void dp(int n, int m)
{
	int g[N][N] = { 0 }, dist[N];
	int path[N] = { 0 }, res[N];
	memset(dist, 0x3f, sizeof dist);
	dist[1] = 0;
	// 读入数据
	for (int i = 1; i < m * n; i++)
	{
		if (i % m == 0)
			continue;
		cin >> g[i][i + 1];
	}

	for (int i = 1; i <= m * (n - 1); i++)
	{
		cin >> g[i][i + m];
	}

	// 动态规划
	for (int i = 2; i <= m; i++)
	{
		dist[i] = dist[i - 1] + g[i - 1][i];
	}

	for (int i = m + 1; i <= n * m; i++)
	{
		if ((i - 1) % m != 0 && dist[i - 1] + g[i - 1][i] <= dist[i - m] + g[i - m][i])
		{
			dist[i] = dist[i - 1] + g[i - 1][i];
			path[i] = i - 1;
		}
		else
		{
			dist[i] = dist[i - m] + g[i - m][i];
			path[i] = i - m;
		}
	}

    // 输出答案
	cout << "需要的时间最短为:" << dist[n * m] << endl << "路径依次是:";

	int j = n * m, i = 0;
	res[i] = n * m;		// 记录终点
	while (path[j] != 0)	// 将路径存放到结果数组中
	{
		res[++i] = path[j];
		j = path[j];
	}
	for (int m = i; m >= 0; m--)	// 逆序输出
	{
		cout << res[m] << " ";
	}
}

int main()
{
	int n, m;		// n代表行数, m代表列数
	cout << "请输入公路矩阵行列的点数" << endl;
	cin >> n >> m;
	cout << "请输入各条边" << endl;
	dp(n, m);
	return 0;
}

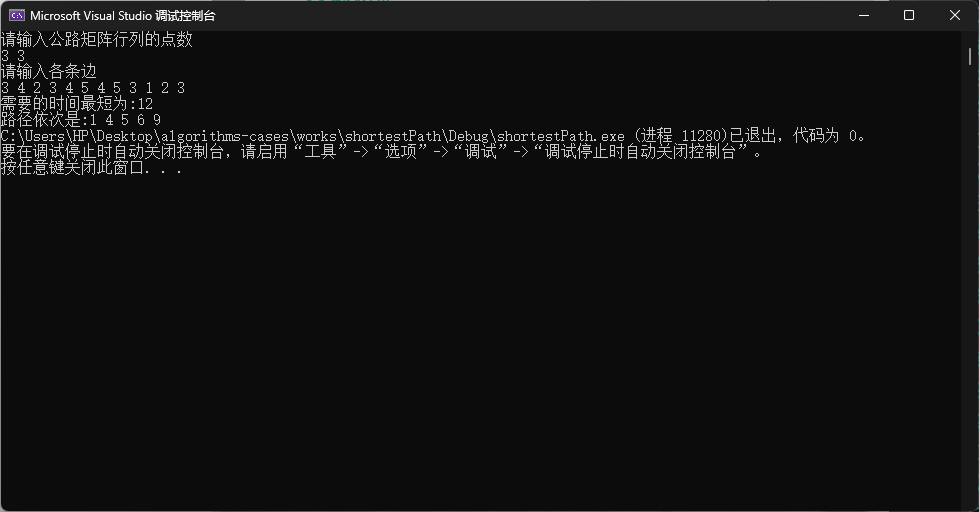
算法实现：

算法需要遍历所有节点，时间复杂度是$O(n)$

问题二

问题描述

在芯片设计中，经常要考虑输入与输出端之间的连接关系，假设输入与输出端分别有若干端口，并且用一组数字进行标注（可能有重复），当且仅当输入端与输出端数字相等并且不与其他连接线相交的情况下，可以建立输入与输出之间的连接。设计算法策略，计算可能得到的最大连接数。

问题分析

这是一道图论的题目，抽象来说，就是在二部图中寻找一个最大的没有交叉连线的匹配，本题的难点在于判断是否存在交叉连线

算法设计

使用递归的深度优先搜索函数dfs用于搜索可能的连接

递归调用中首先检查是否已经遍历完了所有的输出端口，如果是，则更新最大连接数并返回

对于当前输入端口和输出端口集合中的每个输出端口，判断它们的数字是否相等。如果相等，继续判断该连接与已建立的连接是否交叉。若没有交叉，则将该连接添加到当前的连接路径和已建立的连接集合中。

利用dfs的递归性质，穷举所有可能的连接方式，并通过剪枝条件来确保连线不交叉。

// 连接关系结构体
struct Connection {
    int input;
    int output;
};

// 深度优先搜索函数
void dfs(int inputPort, const unordered_set<int>& outputPorts,
         const vector<Connection>& path, int& maxConnections,
         unordered_set<Connection>& connections) {
    if (outputPorts.empty()) {
        maxConnections = max(maxConnections, static_cast<int>(path.size()));
        return;
    }

    for (int outputPort : outputPorts) {
        if (inputPort == outputPort) {
            bool intersects = false;
            for (const Connection& conn : connections) {
                if ((conn.input < inputPort && inputPort < conn.output) ||
                    (conn.input < outputPort && outputPort < conn.output)) {
                    intersects = true;
                    break;
                }
            }
            if (!intersects) {
                vector<Connection> newPath = path;
                newPath.push_back({inputPort, outputPort});
                connections.insert({inputPort, outputPort});
                unordered_set<int> newOutputPorts = outputPorts;
                newOutputPorts.erase(outputPort);
                dfs(inputPort, newOutputPorts, newPath, maxConnections, connections);
                connections.erase({inputPort, outputPort});
            }
        }
    }
}

// 计算最大连接数函数
int calculateMaxConnections(const vector<int>& inputs, const vector<int>& outputs) {
    unordered_set<Connection> connections;
    int maxConnections = 0;

    for (int inputPort : inputs) {
        dfs(inputPort, unordered_set<int>(outputs.begin(), outputs.end()), {},
            maxConnections, connections);
    }

    return maxConnections;
}