问题一
问题描述
Given a tree T = (V,E), find the maximum independent set of the tree. For example, maximum independent set of the tree of following tree has size 7.
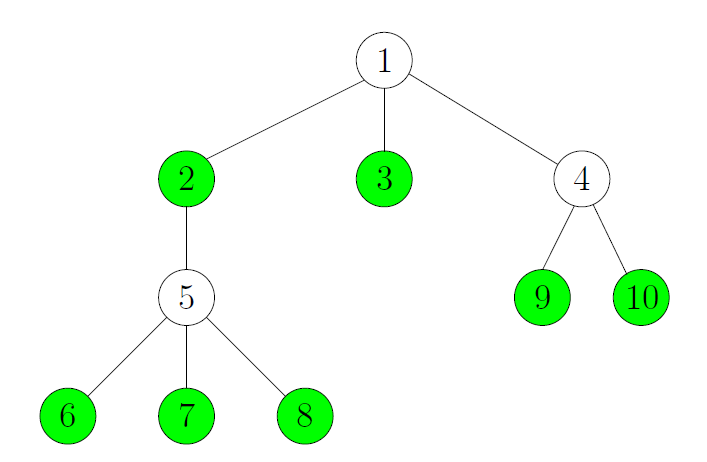
The green vertices shows that the maximum indpendent set of thetree has size 7.
(1) Design an efficient greedy algorithm to solve the problem.
(2) If each vertex has a weight such as benefit,whether can you use a Greedy algorithm to get a maximum benefit where if one vertex has been selected then its adjacent verticex can not be selected.
问题分析
这道思考题考察的是求树中的最大独立集的问题
独立集概念:
对于树$T=(V,E)$,若$V^{‘} \subseteq V$且$V^{‘}$中任意两点都不相邻,则$V^{‘}$是树T的一个独立集
在这个问题中,可以采用贪心算法求取树中的最大独立集
贪心算法通过一系列的局部选择来得到一个问题的解,每一次贪心选择都将所有问题简化为规模更小的子问题。
算法设计
- 初始化一个空的最大独立集
- 从树的叶子节点出发,逐层向上处理。对于每个节点,有两种情况:
- 如果该节点的父结点已经被选中作为最大独立集的一部分,则跳过该节点
- 如果该节点的父结点没有被选中作为最大独立集的一部分,则将该节点添加到最大独立集中,并将其所有子节点标记为已访问
- 当该节点处理完后,向上处理,直到处理完所有节点
使用深度优先搜索遍历树的节点
算法实现
#include <iostream>
#include <vector>
#include <unordered_set>
using namespace std;
struct TreeNode {
int val;
vector<TreeNode*> children;
TreeNode* parent = nullptr;
TreeNode(int value) : val(value) {}
};
unordered_set<TreeNode*> max_independent_set;
unordered_set<TreeNode*> visited;
void dfs(TreeNode* node) {
for (TreeNode* child : node->children) {
dfs(child);
}
if (node->parent && max_independent_set.find(node->parent) == max_independent_set.end() && visited.find(node) == visited.end()) {
max_independent_set.insert(node);
visited.insert(node);
visited.insert(node->parent);
}
}
unordered_set<TreeNode*> findMaxIndependentSet(TreeNode* root) {
max_independent_set.clear();
visited.clear();
dfs(root);
return max_independent_set;
}
int main() {
// 构建树的示例
TreeNode* root = new TreeNode(1);
TreeNode* node2 = new TreeNode(2);
TreeNode* node3 = new TreeNode(3);
TreeNode* node4 = new TreeNode(4);
TreeNode* node5 = new TreeNode(5);
TreeNode* node6 = new TreeNode(6);
TreeNode* node7 = new TreeNode(7);
TreeNode* node8 = new TreeNode(8);
TreeNode* node9 = new TreeNode(9);
root->children.push_back(node2);
root->children.push_back(node3);
root->children.push_back(node4);
node2->parent = root;
node3->parent = root;
node4->parent = root;
node2->children.push_back(node5);
node2->children.push_back(node6);
node5->parent = node2;
node6->parent = node2;
node4->children.push_back(node7);
node4->children.push_back(node8);
node4->children.push_back(node9);
node7->parent = node4;
node8->parent = node4;
node9->parent = node4;
unordered_set<TreeNode*> result = findMaxIndependentSet(root);
// 输出最大独立集中的节点值
for (TreeNode* node : result) {
cout << node->val << " ";
}
cout << endl;
return 0;
}
使用深度优先搜索(DFS)来遍历树的节点。首先,找到所有叶子节点,并从它们的父节点开始逐层向上处理。对于每个节点,如果它的父节点已经被选择,则跳过该节点;否则,将该节点添加到最大独立集中,并将其所有子节点标记为已访问。
这是一个基于贪心算法的近似解法,不一定能够得到最优解。但是,在树结构中,这种贪心算法通常能够得到较好的结果。
算法遍历了整棵树,因此时间复杂度是$O(n)$。
如果在每个顶点都有一个权重时,贪心算法无法保证通过选择顶点使得相邻顶点不能被选择的方式获得最大的收益
贪心算法在每一步都做出局部最优的选择,但是在MWIS问题中,局部最优的选择未必能够得到全局最优解。选择一个顶点意味着排除其相邻的顶点,这种依赖关系使得设计一个能够保证最大收益的贪心算法变得困难。
为了在不能选择相邻顶点的情况下找到最大收益,通常需要其他方法,如动态规划或分支界限算法,这些方法可以探索所有可能的顶点组合以确定最优解。
问题二
问题描述
Scheduling to Minimize Weighted Completion Time
Input: A set of n jobs [n] := {1, 2, 3, · · · , n}, each job j has a weight wj and processing time $t_j$
Output: an ordering of jobs so as to minimize the total weighted completion time of jobs
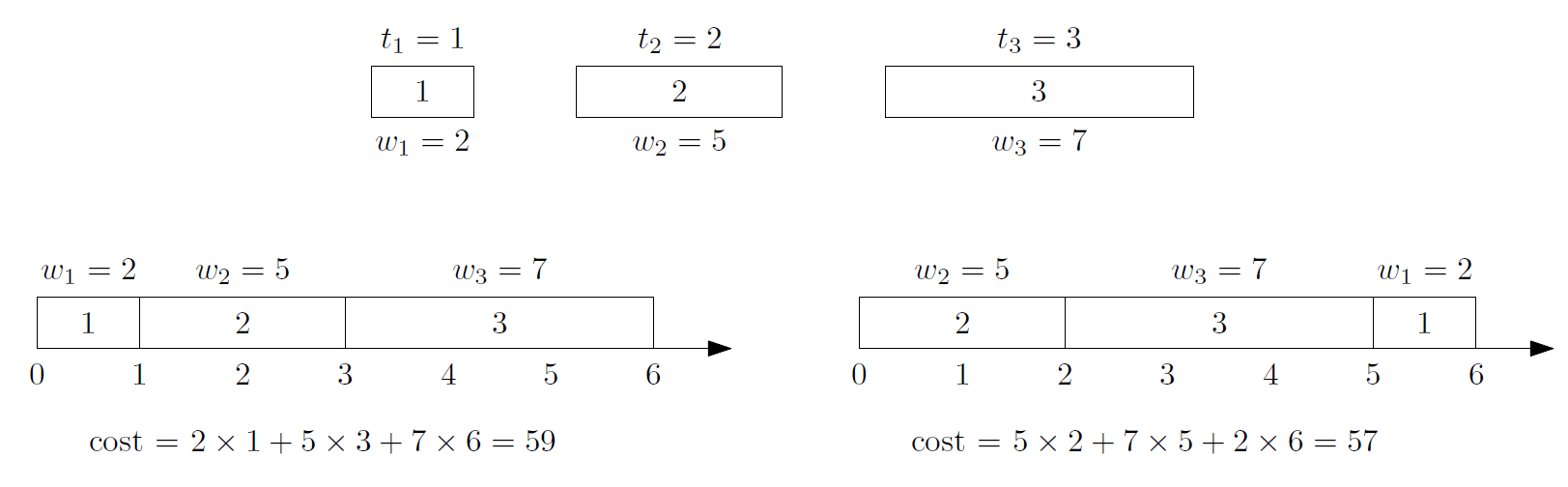
问题分析
解决这道题目可以使用贪心算法,依照某种原则确定执行顺序,在规划工作集的最小权重完成时间时,采用单位时间权重确定优先级
算法设计
要使用贪心算法规划工作集的最小权重完成时间,可以按照以下步骤进行:
定义工作集:给定一组工作,每个工作有一个处理时间和一个权重
排序工作:根据贪心原则,按照某种标准对工作进行排序。一种常见的排序方式是按照权重除以处理时间的比值进行非递增排序(即权重-处理时间比值越大,优先级越高)
创建工作计划:按照排序后的顺序,依次将工作分配给可用的时间槽或机器。可以使用一个变量来记录每个时间槽或机器的当前时间
计算加权完成时间:对于每个已安排的工作,计算其加权完成时间,即该工作的处理时间乘以其权重
计算总加权完成时间:将所有工作的加权完成时间相加,得到最终的总加权完成时间
贪心算法的关键在于选择适当的排序标准,以便每次选择具有最高优先级的工作。然而,需要注意的是,贪心算法并不能保证获得最优解,但可以提供较好的近似解。对于更精确的解,可能需要使用其他算法,如动态规划或整数规划。
算法实现
/*
Scheduling to Minimize Weighted Completion Time
Input: A set of n jobs [n] := {1, 2, 3, · · · , n}, each job j has a weight wj and processing time tj
Output: an ordering of jobs so as to minimize the total weighted completion time of jobs
*/
#include<iostream>
#include<vector>
using namespace std;
struct Job {
int id;
int weight;
int time;
};
void swap(Job& a, Job& b) {
Job temp = a;
a = b;
b = temp;
}
void printjobs(vector<Job>& jobs) {
for (int i = 0; i < jobs.size(); i++) {
cout << jobs[i].id << " " << jobs[i].weight << " " << jobs[i].time << endl;
}
}
void sortjobs(vector<Job>& jobs) {
for (int i = 0; i < jobs.size(); i++) {
for (int j = i + 1; j < jobs.size(); j++) {
if (jobs[i].weight / jobs[i].time < jobs[j].weight / jobs[j].time) {
swap(jobs[i], jobs[j]);
}
}
}
}
int main() {
int n;
cin >> n;
vector<Job> jobs(n);
for (int i = 0; i < n; i++) {
cin >> jobs[i].weight >> jobs[i].time;
jobs[i].id = i + 1;
}
sortjobs(jobs);
printjobs(jobs);
return 0;
}本算法的时间复杂度是$O(n^2)$,改进优先级排序可以做到$O(nlog~n)$的时间复杂度



