学习完经典卷积神经网络,但是经典神经网络并不足以应对当前的计算机视觉要求,继续学习现代卷积神经网络
包括
- AlexNet
- VGG
- NiN
- GoogLeNet
- ResNet
- DenseNet
还将学习批量规范化 batch normalization 和残差网络 ResNet
深度卷积神经网络AlexNet
从对最终模型精度的影响来说,更大或更干净的数据集、或是稍微改进的特征提取,比任何学习算法带来的进步要大得多
学习表征
idea:特征本身应该被学习
在合理的复杂性前提下,特征应该由多个共同学习的神经网络层组成,每个层都有可学习的参数
深度卷积神经网络的突破出现在2012年。突破可归因于两个关键因素:数据、硬件
缺少成分:数据
ImageNet数据集发布,并发起ImageNet挑战赛:要求研究人员从100万个样本中训练模型,以区分1000个不同类别的对象。ImageNet数据集由斯坦福教授李飞飞小组的研究人员开发,利用谷歌图像搜索(Google Image Search)对每一类图像进行预筛选,并利用亚马逊众包(Amazon Mechanical Turk)来标注每张图片的相关类别。这种规模是前所未有的
硬件
GPU的出现,GPU比CPU更适合进行简单计算
处理单元多,带宽高
AlexNet
提供了一个精简版本的AlexNet,取消了并行计算的部分
AlexNet使用了8层卷积神经网络
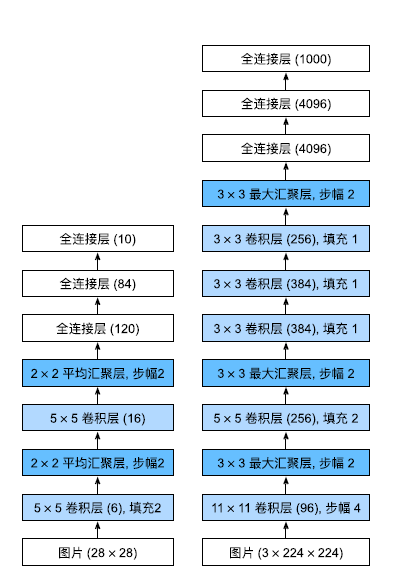
左边是LeNet,右边是AlexNet,设计理念很相似,通过反复卷积提取图像特征
差异:
- AlexNet比相对较小的LeNet5要深得多。AlexNet由八层组成:五个卷积层、两个全连接隐藏层和一个
全连接输出层。 - AlexNet使用ReLU而不是sigmoid作为其激活函数。
模型设计
由于ImageNet中大多数图像的宽高比MNIST大很多,因此需要一个更大的卷积窗口捕获
最后一个卷积层后接三个全连接层
不一样的是原始AlexNet由于显存限制需要双数据流设计,当前GPU的显存充裕不需要跨GPU分解模型
激活函数
使用了ReLU激活函数,很暴力,计算简单,梯度bp的时候也很好计算
池化层
这里用最大池化层替换了平均池化层
容量控制和预处理
通过暂退法控制全连接层的模型复杂度
AlexNet在训练时增加了大量的图像增强数据,如翻转、裁切和变色
import torch
from torch import nn
# 这里设计的AlexNet测试的数据集为MNIST,单通道输入设计
class AlexNet(nn.Module):
def __init__(self):
super().__init__()
self.conv1=nn.Sequential(
nn.Conv2d(1,96,kernel_size=11,stride=4,padding=1),
nn.ReLU(),
nn.MaxPool2d(kernel_size=3,stride=2)
)
self.conv2=nn.Sequential(
nn.Conv2d(96, 256, kernel_size=5, padding=2),
nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2)
)
self.conv3=nn.Sequential(
nn.Conv2d(256, 384, kernel_size=3, padding=1),
nn.ReLU()
)
self.conv4=nn.Sequential(
nn.Conv2d(384, 384, kernel_size=3, padding=1),
nn.ReLU()
)
self.conv5=nn.Sequential(
nn.Conv2d(384, 256, kernel_size=3, padding=1),
nn.ReLU(),
nn.MaxPool2d(kernel_size=3,stride=2)
)
self.flatten=nn.Flatten()
# 使用暂退法减轻过拟合
self.fc1=nn.Sequential(
nn.Linear(256*5*5,4096),
nn.ReLU(),
nn.Dropout(p=0.5)
)
self.fc2=nn.Sequential(
nn.Linear(4096,4096),
nn.ReLU(),
nn.Dropout(p=0.5)
)
self.fc3=nn.Linear(4096,10)
def forward(self, X):
X=self.conv1(X)
X=self.conv2(X)
X=self.conv3(X)
X=self.conv4(X)
X=self.conv5(X)
X=self.flatten(X)
X=self.fc1(X)
X = self.fc2(X)
pred = self.fc3(X)
return pred读取数据集
由于使用Fashion-MNIST/MNIST数据集
将数据集resize成[224,224]就可以使用了
transform=transforms.Compose([
Resize([224,224]),
ToTensor()
])
mnist_training = datasets.MNIST(
root="../data",
train=True,
transform=transform,
download=False
)
mnist_test = datasets.MNIST(
root="../data",
train=False,
transform=transform,
download=False
)其他dataloader没区别。
使用更小的学习速率训练,这是因为网络更深更广、图像分辨率更高,训练卷积神经网络就更昂贵。
AlexNet训练的时候还是比较强的
在第一个epoch的时候loss就降到了小数点后两位,acc 97%+,不过电脑的风扇也是飞快的转,怕扰民第一轮我就把它ban了
epoch 0
---------------------
loss:2.309132 [ 0/ 60000]
loss:2.296461 [ 2560/ 60000]
loss:2.275908 [ 5120/ 60000]
loss:2.206079 [ 7680/ 60000]
loss:1.562011 [10240/ 60000]
loss:1.082462 [12800/ 60000]
loss:0.446683 [15360/ 60000]
loss:0.363827 [17920/ 60000]
loss:0.233036 [20480/ 60000]
loss:0.254791 [23040/ 60000]
loss:0.201992 [25600/ 60000]
loss:0.255451 [28160/ 60000]
loss:0.180451 [30720/ 60000]
loss:0.102079 [33280/ 60000]
loss:0.107142 [35840/ 60000]
loss:0.125804 [38400/ 60000]
loss:0.104566 [40960/ 60000]
loss:0.123582 [43520/ 60000]
loss:0.084459 [46080/ 60000]
loss:0.113914 [48640/ 60000]
loss:0.151553 [51200/ 60000]
loss:0.101548 [53760/ 60000]
loss:0.102417 [56320/ 60000]
loss:0.086216 [58880/ 60000]
test: acc 97.63999938964844
epoch 1
---------------------
loss:0.067266 [ 0/ 60000]
loss:0.113348 [ 2560/ 60000]
loss:0.123024 [ 5120/ 60000]
loss:0.104231 [ 7680/ 60000]
loss:0.094467 [10240/ 60000]
loss:0.055352 [12800/ 60000]
loss:0.101548 [15360/ 60000]
loss:0.051812 [17920/ 60000]
loss:0.074520 [20480/ 60000]
loss:0.048130 [23040/ 60000]
loss:0.030063 [25600/ 60000]
loss:0.107249 [28160/ 60000]
loss:0.097766 [30720/ 60000]
loss:0.036431 [33280/ 60000]
loss:0.033842 [35840/ 60000]
loss:0.075659 [38400/ 60000]
loss:0.057449 [40960/ 60000]
loss:0.042159 [43520/ 60000]
loss:0.114527 [46080/ 60000]
loss:0.051474 [48640/ 60000]
loss:0.018162 [51200/ 60000]
loss:0.025694 [53760/ 60000]
loss:0.036466 [56320/ 60000]
loss:0.108626 [58880/ 60000]
KeyboardInterrupt使用块的网络VGG
从单个神经元的角度思考问题,发展到整个层,现在又转向块,重复层的模式
VGG块
经典卷积神经网络的基本组成部分:
- 带填充以保持分辨率的卷积层;
- 非线性激活函数,如ReLU;
- 汇聚层,如最大汇聚层
VGG块就是上述三个层组成的一个块
使用了带有$3 \times 3$卷积核、填充为1(保持高度和宽度)的卷积层,和带有$2 \times 2$汇聚窗口、步幅为2(每个块后的分辨率减半)的最大汇聚层。
吃个栗子
用函数定义一个VGG块
import torch
from torch import nn
def vgg_block(num_convs,in_channels,out_channels):
layers=[]
for _ in range(num_convs):
layers.append(nn.Conv2d(in_channels,out_channels,kernel_size=3,padding=1))
layers.append(nn.ReLU())
in_channels=out_channels
layers.append(nn.MaxPool2d(kernel_size=2,stride=2))
return nn.Sequential(*layers)VGG网络
与AlexNet、LeNet一样,VGG网络可以分为两部分:第一部分主要由卷积层和汇聚层组成,第二部分由全连接层组成
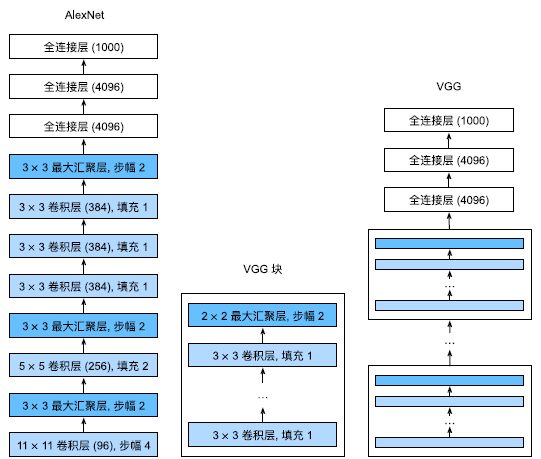
其中有超参数变量conv_arch。该变量指定了每个VGG块里卷积层个数和输出通道数
原始VGG网络有5个卷积块,其中前两个块各有一个卷积层,后三个块各包含两个卷积层。第一个模块有64个输出通道,每个后续模块将输出通道数量翻倍,直到该数字达到512。
由于该网络使用8个卷积层和3个全连接层,因此它通常被称为VGG‐11。
吃个栗子
实现一个VGG-11
conv_arch=(
(1,64),
(1,128),
(2,256),
(2,512),
(2,512)
)def VGG(conv_arch):
conv_blks=[]
in_channels=1
for (num_convs,out_channels) in conv_arch:
conv_blks.append(
vgg_block(num_convs,in_channels,out_channels)
)
in_channels=out_channels
out_channels=conv_arch[-1][1]
return nn.Sequential(
*conv_blks,
nn.Flatten(),
nn.Linear(out_channels*7*7,4096),
nn.ReLU(),nn.Dropout(0.5),
nn.Linear(4096,4096),
nn.ReLU(),nn.Dropout(0.5),
nn.Linear(4096,10)
)和AlexNet训练使用相同的训练框架
epoch 0
---------------------
loss:2.301156 [ 0/ 60000]
loss:2.305832 [ 1280/ 60000]
loss:2.296857 [ 2560/ 60000]
loss:2.292382 [ 3840/ 60000]
loss:2.287944 [ 5120/ 60000]
loss:2.267069 [ 6400/ 60000]
loss:2.118567 [ 7680/ 60000]
loss:1.240553 [ 8960/ 60000]
loss:0.611455 [10240/ 60000]
loss:0.658462 [11520/ 60000]
loss:0.460682 [12800/ 60000]
loss:0.242844 [14080/ 60000]
loss:0.177017 [15360/ 60000]
loss:0.355205 [16640/ 60000]
loss:0.213276 [17920/ 60000]
loss:0.168332 [19200/ 60000]
loss:0.160125 [20480/ 60000]
loss:0.121496 [21760/ 60000]
loss:0.278805 [23040/ 60000]
loss:0.179440 [24320/ 60000]
loss:0.137964 [25600/ 60000]
loss:0.183054 [26880/ 60000]
loss:0.099813 [28160/ 60000]
loss:0.080487 [29440/ 60000]
loss:0.098885 [30720/ 60000]
loss:0.245040 [32000/ 60000]
loss:0.109399 [33280/ 60000]
loss:0.112814 [34560/ 60000]
loss:0.053773 [35840/ 60000]
loss:0.126897 [37120/ 60000]
loss:0.098267 [38400/ 60000]
loss:0.057795 [39680/ 60000]
loss:0.085521 [40960/ 60000]
loss:0.037295 [42240/ 60000]
loss:0.158164 [43520/ 60000]
loss:0.140845 [44800/ 60000]
loss:0.108891 [46080/ 60000]
loss:0.032962 [47360/ 60000]
loss:0.118958 [48640/ 60000]
loss:0.069258 [49920/ 60000]
loss:0.096337 [51200/ 60000]
loss:0.238867 [52480/ 60000]
loss:0.059034 [53760/ 60000]
loss:0.049489 [55040/ 60000]
loss:0.080771 [56320/ 60000]
loss:0.027918 [57600/ 60000]
loss:0.065127 [58880/ 60000]
test: acc 97.86000061035156
epoch 1
---------------------
loss:0.027624 [ 0/ 60000]
loss:0.102138 [ 1280/ 60000]
loss:0.027850 [ 2560/ 60000]
loss:0.023309 [ 3840/ 60000]网络中的网络NiN
在每个像素的通道上分别使用多层感知机
NiN块
卷积层的输入和输出由四维张量组成,张量的每个轴分别对应样本、通道、高度和宽度
NiN的想法是在每个像素位置(针对每个高度和宽度)应用一个全连接层
将权重连接到每个空间位置,可以将其视为$1 \times 1$卷积层,或作为在每个像素位置上独立作用的全连接层
从另一个角度看,即将空间维度中的每个像素视为单个样本,将通道维度视为不同特征(feature)。
NiN块以一个普通卷积层开始,后面是两个$1 \times 1$的卷积层。这两个$1 \times 1$卷积层充当带有ReLU激活函数的逐像素全连接层。第一层的卷积窗口形状通常由用户设置。随后的卷积窗口形状固定为$1 \times 1$。
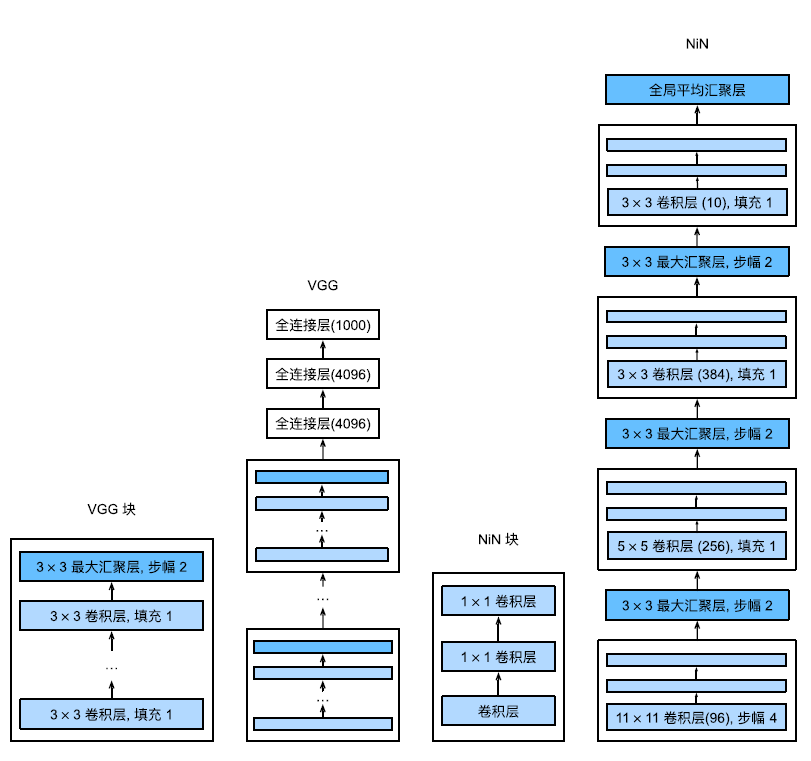
NiN模型
最初的NiN网络是在AlexNet后不久提出的,从AlexNet中得到启发,NiN块窗口形状和AlexNet相似,输出通道数量与AlexNet中的相同,每个NiN块后有一个最大汇聚层。
值得关注的是NiN完全取消了全连接层
NiN使用一个NiN块,其输出通道数等于标签类别的数量。最后放一个全局平均汇聚层(global average pooling layer),生成一个对数几率(logits),显著减少了模型所需参数的数量
吃个栗子
实现NiN网络
import torch
from torch import nn
def nin_block(in_channels, out_channels, kernel_size, strides, padding):
return nn.Sequential(
nn.Conv2d(in_channels, out_channels, kernel_size, strides, padding),
nn.ReLU(),
nn.Conv2d(out_channels, out_channels, kernel_size=1), nn.ReLU(),
nn.Conv2d(out_channels, out_channels, kernel_size=1), nn.ReLU()
)
class NiN(nn.Module):
def __init__(self):
super().__init__()
self.nin1 = nin_block(1, 96, 11, 4, 0)
self.nin2 = nin_block(96, 256, 5, 1, 2)
self.nin3 = nin_block(256, 384, 3, 1, 1)
self.nin4 = nin_block(384, 10, 3, 1, 1)
self.maxPool2d = nn.MaxPool2d(kernel_size=3, stride=2)
self.adaptiveAvgPool2d = nn.AdaptiveAvgPool2d((1, 1))
self.flatten = nn.Flatten()
self.dropout = nn.Dropout(0.5)
def forward(self, X):
X = self.nin1(X)
X = self.maxPool2d(X)
X = self.nin2(X)
X = self.maxPool2d(X)
X = self.nin3(X)
X = self.maxPool2d(X)
X = self.dropout(X)
X = self.nin4(X)
pred = self.flatten(X)
return pred含并行连结的网络GoogLeNet
一个稍微简化的GoogLeNet版本:省略了一些为稳定训练而添加的特殊特性,现在有了更好的训练方法,这些特性不是必要的。
Inception块
在GoogLeNet中,基本的卷积块被称为Inception块(Inception block)
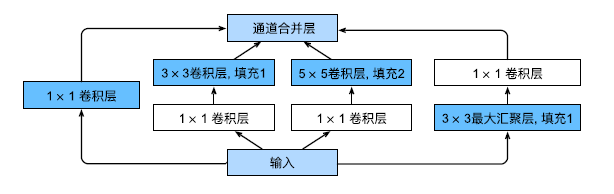
Inception块由四条并行路径组成
这四条路径都使用合适的填充来使输入与输出的高和宽一致,最后我们将每条线路的输出在通道维度上连结,并构成Inception块的输出。
在Inception块中,通常调整的超参数是每层输出通道数。
GoogLeNet模型
GoogLeNet一共使用9个Inception块和全局平均汇聚层的堆叠来生成其估计值。Inception块之间的最大汇聚层可降低维度。第一个模块类似于AlexNet和LeNet,Inception块的组合从VGG继承,全局平均汇聚层避免了在最后使用全连接层
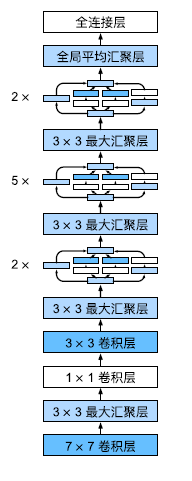
这一个模型还是比较复杂的,在Inception块的超参数设置方面存在一定难度
吃个栗子
实现一个GoogLeNet
import torch
from torch import nn
from Inception import Inception
class GoogLeNet(nn.Module):
def __init__(self):
super(GoogLeNet, self).__init__()
self.b1 = nn.Sequential(
nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1)
)
self.b2 = nn.Sequential(
nn.Conv2d(64, 64, kernel_size=1),
nn.ReLU(),
nn.Conv2d(64, 192, kernel_size=3, padding=1),
nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1)
)
self.b3 = nn.Sequential(
Inception(192, 64, (96, 128), (16, 32), 32),
Inception(256, 128, (128, 192), (32, 96), 64),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1)
)
self.b4 = nn.Sequential(
Inception(480, 192, (96, 208), (16, 48), 64),
Inception(512, 160, (112, 224), (24, 64), 64),
Inception(512, 128, (128, 256), (24, 64), 64),
Inception(512, 112, (144, 288), (32, 64), 64),
Inception(528, 256, (160, 320), (32, 128), 128),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1)
)
self.b5 = nn.Sequential(
Inception(832, 256, (160, 320), (32, 128), 128),
Inception(832, 384, (192, 384), (48, 128), 128),
nn.AdaptiveAvgPool2d((1, 1)),
nn.Flatten()
)
self.fc = nn.Linear(1024, 10)
def forward(self, x):
x = self.b1(x)
x = self.b2(x)
x = self.b3(x)
x = self.b4(x)
x = self.b5(x)
pred = self.fc(x)
return pred
批量规范化
批量规范化可持续加速深层网络的收敛速度
训练深层网络
数据预处理的方式通常会对最终结果产生巨大影响
批量规范化的发明者非正式地假设,这些变量分布中的这种偏移可能会阻碍网络的收敛
更深层的网络很复杂,容易过拟合,这意味着正则化变得更加重要
批量规范化应用于单个可选层(也可以应用到所有层),其原理如下:在每次训练迭代中,我们首先规范化输入,即通过减去其均值并除以其标准差,其中两者均基于当前小批量处理。接下来,我们应用比例系数和比例偏移。正是由于这个基于批量统计的标准化,才有了批量规范化的名称
$\mathbf{x}\in{\mathcal{B}}$表示来自小批量B的输入,批量规范化BN根据以下表达式转换x
$$
\mathrm{BN}(\mathbf{x})=\gamma\odot\frac{\mathbf{x}-\hat{\mu}{\mathcal{B}}}{\hat{\sigma}{\mathcal{B}}}+\beta
$$
其中$\gamma,\beta$是需要与其他模型参数一起学习的参数
$$
\begin{aligned}
&\hat{\mu}{\mathcal{B}} =\frac{1}{|{\mathcal B}|}\sum{\mathbf{x}\in{\mathcal B}}\mathbf{x}, \
&\hat{\sigma}{B}^{2} =\frac{1}{|\mathcal{B}|}\sum{\mathbf{x}\in\mathcal{B}}(\mathbf{x}-\hat{\mu}_{\mathcal{B}})^{2}+\epsilon.
\end{aligned}
$$
方差添加小常量确保不除以零
优化中的各种噪声源通常会导致更快的训练和较少的过拟合:这种变化似乎是正则化的一种形式
批量规范化层在”训练模式“(通过小批量统计数据规范化)和“预测模式”(通过数据集统计规范化)中的功能不同。
在训练过程中,我们无法得知使用整个数据集来估计平均值和方差,所以只能根据每个小批次的平均值和方差不断训练模型。而在预测模式下,可以根据整个数据集精确计算批量规范化所需的平均值和方差
批量规范化层
全连接层的批量规范化
$$
\mathbf{h}=\phi(\mathrm{BN}(\mathbf{W}\mathbf{x}+\mathbf{b}))
$$
卷积层的批量规范化
需要对这些通道的“每个”输出执行批量规范化,每个通道都有自己的拉伸(scale)和偏移(shift)参数,这两个参数都是标量
从零实现
吃个栗子
实现一个具有张量的批量规范化层
import torch
from torch import nn
def batch_norm(X,gamma,beta,moving_mean,moving_var,eps,momentum):
if not torch.is_grad_enabled():
X_hat=(X-moving_mean)/torch.sqrt(moving_var+eps)
else:
assert len(X.shape) in (2,4)
if len(X.shape)==2:
mean=X.mean(dim=0)
var=((X-mean)**2).mean(dim=0)
else:
mean=X.mean(dim=(0,2,3),keepdim=True)
var=((X-mean)**2).mean(dim=(0,2,3),keepdim=True)
X_hat=(X-mean)/torch.sqrt(var+eps)
moving_mean=momentum*moving_mean+(1.0-momentum)*mean
moving_var=momentum*moving_var+(1.0-momentum)*var
Y=gamma*X_hat+beta
return Y,moving_mean.data,moving_var.data批量规范化层的LeNet
net=nn.Sequential(
nn.Conv2d(1,6,5),
BatchNorm(6,num_dims=4),
nn.Sigmoid(),
nn.MaxPool2d(2,2),
nn.Conv2d(6,16,5),
BatchNorm(16,num_dims=4),
nn.Sigmoid(),
nn.MaxPool2d(2,2),
nn.Flatten(),
nn.Linear(16*4*4,120),
BatchNorm(120,num_dims=2),
nn.Sigmoid(),
nn.Linear(120,84),
BatchNorm(84,num_dims=2),
nn.Sigmoid(),
nn.Linear(84,10)
)简明实现
net=nn.Sequential(
nn.Conv2d(1,6,5),
nn.BatchNorm2d(6),
nn.Sigmoid(),
nn.MaxPool2d(2,2),
nn.Conv2d(6,16,5),
nn.BatchNorm2d(16),
nn.Sigmoid(),
nn.MaxPool2d(2,2),
nn.Flatten(),
nn.Linear(16*4*4,120),
nn.BatchNorm1d(120),
nn.Sigmoid(),
nn.Linear(120,84),
nn.BatchNorm1d(84),
nn.Sigmoid(),
nn.Linear(84,10)
)争议
批量规范化被认为可以使优化更加平滑
通过减少内部协变量偏移(internal covariate shift)。
残差网络ResNet
函数类
$$
f_{\mathcal{F}}^*:=\underset{f}{\operatorname*{argmin}}L(\mathbf{X},\mathbf{y},f)\text{ subject to }f\in\mathcal{F}
$$
找到一个函数使得差距最凶啊
对于非嵌套函数(non‐nested function)类,较复杂的函数类并不总是向“真”函数$f∗$靠拢
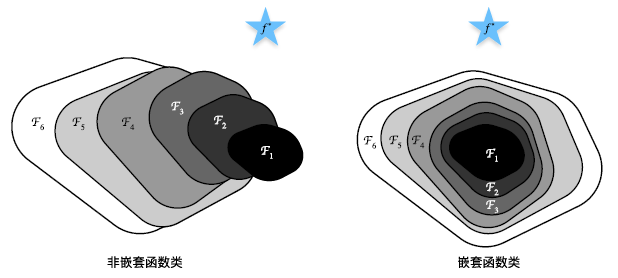
如果我们能将新添加的层训练成恒等映射(identity function)$f(x) = x$,新模型和原模型将同样有效。
残差网络的核心思想是:每个附加层都应该更容易地包含原始函数作为其元素之一
残差块
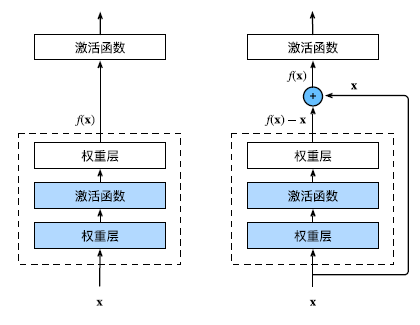
正常块和残差块
ResNet沿用了VGG完整的$3 \times 3$卷积层设计。
吃个栗子
实现残差块
class Residual(nn.Module):
def __init__(self, input_channels, num_channels, use_1x1conv=False, strides=1):
super().__init__()
self.conv1 = nn.Conv2d(input_channels, num_channels, kernel_size=3, padding=1, stride=strides)
self.conv2 = nn.Conv2d(num_channels, num_channels, kernel_size=3, padding=1)
if use_1x1conv:
self.conv3 = nn.Conv2d(input_channels, num_channels, kernel_size=1, stride=strides)
else:
self.conv3 = None
self.bn = nn.BatchNorm2d(num_channels)
self.relu = nn.ReLU()
def forward(self, X):
Y = self.relu(self.bn(self.conv1(X)))
Y = self.bn(self.conv2(Y))
if self.conv3:
X = self.conv3(X)
Y += X
return self.relu(Y)ResNet
ResNet前两层结构和GoogLeNet一样
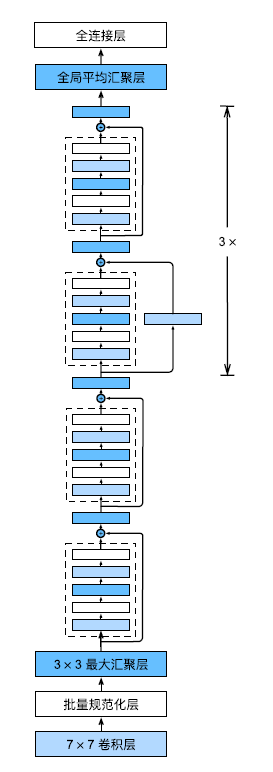
ResNet-18架构
def resnet_block(input_channels, num_channels, num_residuals, first_block=False):
blk = []
for i in range(num_residuals):
if i == 0 and not first_block:
blk.append(
Residual(input_channels, num_channels, use_1x1conv=True, strides=2)
)
else:
blk.append(
Residual(num_channels, num_channels)
)
return blk
class ResNet(nn.Module):
def __init__(self):
super().__init__()
self.b1 = nn.Sequential(
nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
nn.BatchNorm2d(64),
nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1)
)
self.b2 = nn.Sequential(*resnet_block(64, 64, 2, first_block=True))
self.b3 = nn.Sequential(*resnet_block(64, 128, 2))
self.b4 = nn.Sequential(*resnet_block(128, 256, 2))
self.b5 = nn.Sequential(*resnet_block(256, 512, 2))
self.adaptiveAvgPool2d = nn.AdaptiveAvgPool2d((1, 1))
self.flatten = nn.Flatten()
self.fc = nn.Linear(512, 10)
def forward(self,X):
X=self.b1(X)
X = self.b2(X)
X = self.b3(X)
X = self.b4(X)
X = self.b5(X)
X=self.adaptiveAvgPool2d(X)
X=self.flatten(X)
pred=self.fc(X)
return pred稠密链接网络DenseNet
从ResNet到DenseNet
ResNet将f分解为两部分:一个简单的线性项和一个复杂的非线性项
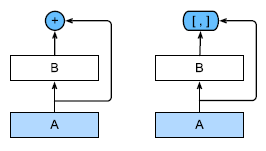
ResNet和DenseNet的关键区别在于,DenseNet输出是连接(用图中的[, ]表示)而不是
如ResNet的简单相加。因此,在应用越来越复杂的函数序列后,我们执行从x到其展开式的映射:
$$
\mathbf{x}\to[\mathbf{x},f_1(\mathbf{x}),f_2([\mathbf{x},f_1(\mathbf{x})]),f_3([\mathbf{x},f_1(\mathbf{x}),f_2([\mathbf{x},f_1(\mathbf{x})])]),\ldots]
$$
最后,将这些展开式结合到多层感知机中,再次减少特征的数量。实现起来非常简单:我们不需要添加术语,而是将它们连接起来
稠密块体
一个稠密块由多个卷积块组成,每个卷积块使用相同数量的输出通道。然而,在前向传播中,我们将每个卷积块的输入和输出在通道维上连结。
def conv_block(input_channels, num_channels):
return nn.Sequential(
nn.BatchNorm2d(input_channels), nn.ReLU(),
nn.Conv2d(input_channels, num_channels, kernel_size=3, padding=1))
class DenseBlock(nn.Module):
def __init__(self, num_convs, input_channels, num_channels):
super(DenseBlock, self).__init__()
layer = []
for i in range(num_convs):
layer.append(conv_block(num_channels * i + input_channels, num_channels))
self.net = nn.Sequential(*layer)
def forward(self, X):
for blk in self.net:
Y = blk(X)
# 连接通道维度上每个块的输入和输出
X = torch.cat((X, Y), dim=1)
return X过渡层
由于每个稠密块都会带来通道数的增加,使用过多则会过于复杂化模型。而过渡层可以用来控制模型复杂度。它通过$1 \times 1$卷积层来减小通道数,并使用步幅为2的平均汇聚层减半高和宽,从而进一步降低模型复杂度。
def transition_block(input_channels, num_channels):
return nn.Sequential(
nn.BatchNorm2d(input_channels), nn.ReLU(),
nn.Conv2d(input_channels, num_channels, kernel_size=1),
nn.AvgPool2d(kernel_size=2, stride=2))DenseNet模型
b1 = nn.Sequential(
nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
nn.BatchNorm2d(64), nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
num_channels, growth_rate = 64, 32
num_convs_in_dense_blocks = [4, 4, 4, 4]
blks = []
for i, num_convs in enumerate(num_convs_in_dense_blocks):
blks.append(DenseBlock(num_convs, num_channels, growth_rate))
# 上一个稠密块的输出通道数
num_channels += num_convs * growth_rate
# 在稠密块之间添加一个转换层,使通道数量减半
if i != len(num_convs_in_dense_blocks) - 1:
blks.append(transition_block(num_channels, num_channels // 2))
num_channels = num_channels // 2
net = nn.Sequential(
b1, *blks,
nn.BatchNorm2d(num_channels), nn.ReLU(),
nn.AdaptiveAvgPool2d((1, 1)),
nn.Flatten(),
nn.Linear(num_channels, 10))


