总结一下一些常见的损失函数以及实现方式
参考文献:A survey and taxonomy of loss functions in machine learning
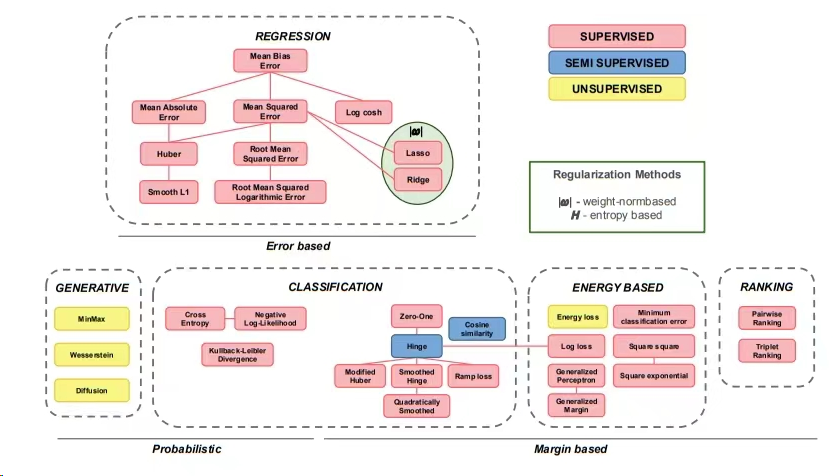
loss function分类法
适应任务的损失分类
- 回归
- 分类
- 生成模型
- 排序
- 非归一化概率模型(基于能量的模型)
数学概念的损失分类
- 基于错误的
- 概率
- 基于间隔的
损失函数的一些性质
- 连续性CONT
- 可微性DIFF
- 李普希兹连续性L-CONT
- 凸性CONV
- 严格凸S-CONV
通过损失增强进行正则化
$$
\widehat L(f(\mathbf{x}_i),\mathbf{y}_i)=L(f(\mathbf{x}_i),\mathbf{y}_i)+\lambda\rho(\mathbf{\Theta})
$$
L1正则化
$$
\rho(\Theta)=|\Theta|_{2}^{2}
$$
L2正则化
$$
\rho(\Theta)=|\Theta|
$$
回归损失
回归损失的模型是为了基于一个或多个前因变量x的值预测连续变量y的输出
回归模型的最终目标是通过最小化某一损失函数估计模型的参数使得输出拟合原始数据
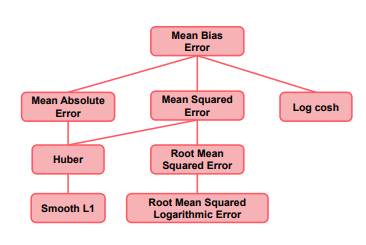
所有回归任务的损失基于残差函数,也就是观测值和预测值之间的不同
MBE、MAE、MSE、RMSE
Huber loss、smooth L1
Los-cosh、RMSLE
Mean Bias Error Loss
CONT,DIFF
$$
\mathcal{L}{MBE}=\frac{1}{N}\sum{i=1}^{N}y_i-f(\mathbf{x}_i)
$$
MBE很少用于训练回归模型,因为正误差与负误差相互抵消
与MBE直接相关的有MAE,MSE,Log-cosh,差别就在于如何挖掘偏差
Mean Absolute Error Loss
L-CONT,CONV
$$
\mathcal{L}{MAE}=\frac{1}{N}\sum{i=1}^{N}|y_{i}-f(\mathbf{x}_{i})|
$$
MAE或者L1损失是最基础的回归损失函数
偏置取绝对值克服了正负误差抵消问题
梯度大小并不取决于误差大小,当误差小的时候会导致模型的收敛问题
当以输入为条件的目标数据是对称的时,训练以最小化 MAE 的模型更有效。
需要强调的是,绝对值为零的导数没有定义。
MAE也用来评估模型的表现
Mean Squared Error Loss
CONT,DIFF,CONV
$$
\mathcal{L}{MSE}=\frac{1}{N}\sum{i=1}^{N}\left(y_{i}-f(\mathbf{x}_{i})\right)^{2}
$$
平方项使所有偏差为正,并放大了异常值的贡献,使其更适合观测值中噪声服从正态分布的问题。
主要缺点是对异常值的敏感性。
Root Mean Squared Error Loss
CONT,DIFF,CONV
$$
\mathcal{L}{RMSE}=\sqrt{\frac{1}{N}\sum{i=1}^N\left(y_i-f(\mathbf{x}_i)\right)^2}
$$
确保损失具有与感兴趣变量相同的单位和规模
由于MSE与RMSE只相差一个开根操作,最小互操作会是模型收敛到相同的优化值
也用来评估模型的表现,并有相同的限制条件
Huber Loss
L-CONT,DIFF,S-CONV
$$
L_{Huberloss}=\left{\begin{matrix}\frac{1}{2}\left(y_i-f(\mathbf{x}_i)\right)^2&for\left|y_i-f(\mathbf{x}_i)\right|\leq\delta,\\delta\left(\left|y_i-f(\mathbf{x}_i)\right|-\frac{1}{2}\delta\right)&otherwise\end{matrix}\right.
$$
综合了MAE、MSE
能够结合MAE和MSE的优点,当模型的预测和输出之间的差异是巨大的误差是线性的时,使Huber损失对异常值的敏感度降低
huber loss的限制点在于有额外的超参数
当$\delta=1$时,得到smooth L1 loss
Log-cosh loss
CONT,DIFF
$$
\mathcal{L}{logcosh}=\frac{1}{N}\sum{i=1}^{N}log\left(cosh\left(f(\mathbf{x}{i})-y{i}\right)\right)
$$
对数余弦损失是观测值之间残差的双曲余弦的对数
无需设置超参数,但代价是计算成本更高
在任何地方都可以微分两次,这使得它适用于需要求解二阶导数的方法
与huber loss相比,不能调参了
Root Mean Squared Logarithmic Error Loss
CONT,DIFF,CONV
$$
\mathcal{L}{RMSLE}=\sqrt{\frac{1}{N}\sum{i=1}^{N}\left(\log(y_{i}+1)-\log(f(\mathbf{x}_{i})+1)\right)^{2}}
$$
预测值和实际值之间的误差是相对的,这使得 RMSLE 对异常值更具鲁棒性
RMSLE 适用于目标具有指数关系的问题,或者最好惩罚低估的而不是高估的
损失不适用于允许负值的问题
分类损失
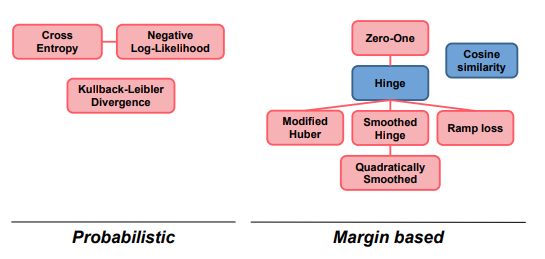
分类的目标时将输入x分配到K个离散的类中
包括两种方式,直接预测标签或者返回标签的概率
基于间隔的
- Zero-One loss
- Hinge loss
- Smoothed Hinge loss
- Quadratically Smoothed Hinge loss
- Modified Huber loss
- Ramp loss
- Cosine Similarity loss
基于概率
- Cross Entropy loss
- Negative Log-Likelihood loss
- Kullback-Leibler Divergence loss
基于margin的损失函数
Zero-One loss
$$
L_{\text{ZeroOne}}(f(\mathbf{x}),y)=\begin{cases}1&\text{if}f(\mathbf{x})\cdot y<0\0&\text{otherwise}\end{cases}
$$
Zero-One loss不能直接使用,因为它缺乏凸性和可微性
Hinge loss and Perceptron loss
L-CONT,CONV
$$
L_{\mathrm{Hinge}}(f(\mathbf{x}),y)=\max(0,1-(f(\mathbf{x})\cdot y))
$$
不严格凸,hinge loss多用于SVM支持向量机
感知器损失
$$
L_\text{Perceptron}(f(\mathbf{x}),y)=\max(0,-(f(\mathbf{x})\cdot y))
$$
它不会惩罚边缘内的样本,围绕分离的超平面,而只是那些被该超平面错误标记的样本,具有相同的线性惩罚
模型对训练数据中的异常值敏感,且不连续可微
Smoothed Hinge Loss
L-CONT,CONV
$$
L_\text{SmoothedHinge}(f(\mathbf{x}),y)=\begin{cases}\frac{1}{2}-(f(\mathbf{x})\cdot t)&(f(\mathbf{x})\cdot y)<=0\\frac{1}{2}(1-(f(\mathbf{x})\cdot t))^2&0<(f(\mathbf{x})\cdot y)<1\0&(f(\mathbf{x})\cdot y)>=1\end{cases}
$$
这种损失继承了原始hinge loss对异常值的敏感性
Quadratically Smoothed Hinge loss
L-CONT,CONV,DIFF
$$
L_\text{QSmoothedHinge}(f(\mathbf{x}),y)=\begin{cases}\frac{1}{2\gamma}\max(0,-(f(\mathbf{x})\cdot y))^2&(f(\mathbf{x})\cdot y)>=1-\gamma\1-\frac{\gamma}{2}-(f(\mathbf{x})\cdot y)&\text{otherwise}\end{cases}
$$
超参数决定了平滑度,$\gamma \to 0$成为原始hinge,但是全域不可微
Modified Huber loss
L-CONT, DIFF, S-CONV
$$
L_\text{ModHuber}(f(\mathbf{x}),y)=\begin{cases}\frac{1}{4}\max(0,-(f(\mathbf{x})\cdot y))^2&(f(\mathbf{x})\cdot y)>=-1\-(f(\mathbf{x})\cdot y)&\text{otherwise}\end{cases}
$$
$\gamma=2$
Ramp Loss
CONT,CONV
$$
L_{\text{Ramp}}(f(\mathbf{x}),y)=\begin{cases}L_{\text{Hinge}}(f(\mathbf{x}),y))&(f(\mathbf{x})\cdot y)<=1\1&\text{otherwise}\end{cases}
$$
在SVM中会生成使用更小、更稳定的支持向量集的支持向量机
Cosine Similarity loss
L-CONT,DIFF
$$
L_{cos-sim}(f(\mathbf{x}),\mathbf{y})=1-\frac{\mathbf{y}\cdot\mathbf{f}(\mathbf{x})}{|\mathbf{y}||\mathbf{f}(\mathbf{x})|}
$$
当向量的大小不重要时,余弦相似度通常用作测量距离的度量
限制在[-1,1]
概率损失函数
Cross Entropy loss and Negative Log-Likelihood loss
CONT,DIFF,CONV
极大似然估计(MLE)是一种通过极大化似然来估计概率分布参数的方法
MLE可以被认为是极大a-后验估计(MAP)的特例
对数似然
$$
log(P(\mathcal{D}|\Theta))=\sum_{i=1}^N(y_i\log(f_\Theta(\mathbf{x}i))+(1-y_i)\log(1-f_\Theta(\mathbf{x}i))))
$$
负对数似然=交叉熵损失
$$
\mathcal{L}{NLL}=-\sum{i=1}^N(y_i\log(f_\Theta(\mathbf{x}i))+(1-y_i)\log(1-f_\Theta(\mathbf{x}i)))
$$
K类交叉熵损失
$$
L{CCE}=-\frac{1}{K}\sum{j=1}^{K}\log(\widehat{f_{k}}(\mathbf{x}))
$$
$$
\widehat{f_k}(\mathbf{x}_i)=f_S(f_k(\mathbf{x}))
$$
$f_S$是softmax函数
Kullback-Leibler divergence
CONT, CONV, DIFF
KL散度,是对一种概率分布与另一种概率分布的不同之处的非对称测量
$$
\mathrm{KL}(q||f_{\Theta})=\int q(\mathbf{x})\log(\frac{q(\mathbf{x})}{f_{\Theta}(\mathbf{x})})d\mathbf{x}=-\int q(\mathbf{x})\log(f_{\Theta}(\mathbf{x}))d\mathbf{x}+\int q(\mathbf{x})\log(q(\mathbf{x}))d\mathbf{x}
$$
$$
\min_{\Theta}\mathrm{KL}(q||f_{\Theta})=\min_{\Theta}-\int q(\mathbf{x})\log(f_{\Theta}(\mathbf{x}))d\mathbf{x}=\min_{\Theta}H(q,f_{\Theta})
$$
分类最好使用交叉熵损失而不是KL散度



