看一下近年dl的祖师爷之作——变形金刚
先验知识
BLEU
Bilingual Evaluation Understudy
双语评估替补
评估模型生成的句子(candidate)和实际句子(reference)的差异的指标
取值范围$[0.0-1.0]$
- 计算代价小
- 易理解
- 语言无关
- 与人类评价高度相关
- 广泛应用
Bleu: a Method for Automatic Evaluation of Machine Translation - ACL Anthology
循环神经网络的欠缺
循环神经网络要点在于隐藏层计算,前一个隐藏层变量$h_{t-1}$和当前位置$t$计算出当前位置隐藏变量$h_t$。这种内在的顺序性是的在训练示例中无法实现并行,而这在较长的序列长度上变得至关重要,因为内存容量限制了跨示例的批处理
以前的attention机制只和循环神经网络结合,而我们的变形金刚transformer,摒弃了循环神经网络,完全依赖于注意力机制,在输入、输出之间建立全局依赖关系。
Transformer架构
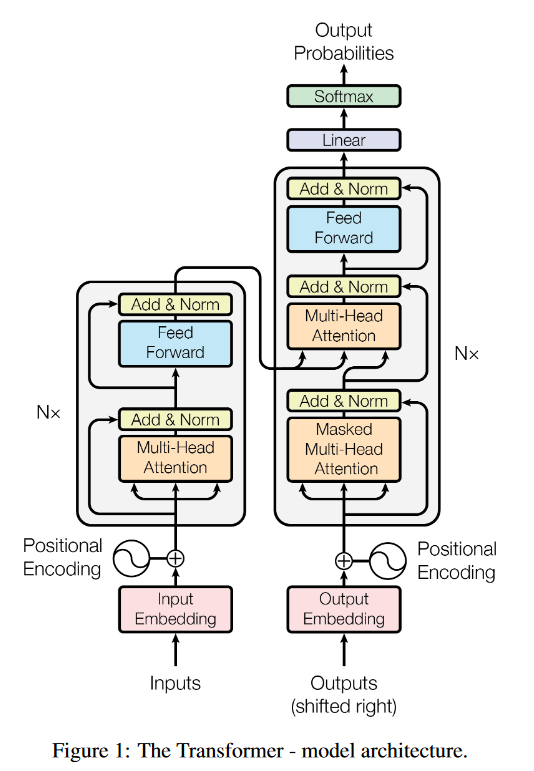
encoder和decoder
编码器是左边一块,解码器是右边一块
编码器的工作流是:input embedding->多头注意力->残差+规范化->前馈(全连接层)->残差+规范化
解码器的工作流有一块其实和编码器很像,添加了一块output embedding和masked多头注意力
masked多头注意力机制与偏移一个位置的output embedding相结合,确保位置i的预测只能依赖于小于i位置的已知输出。
attention
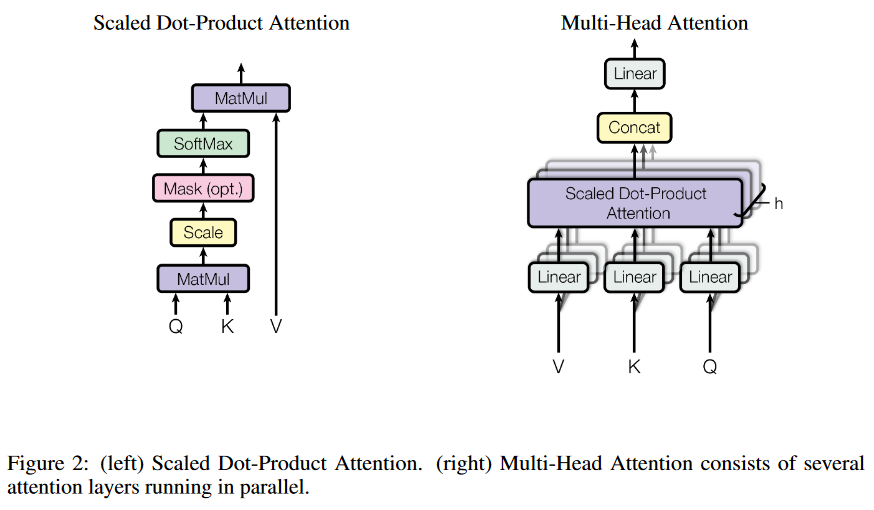
attention那就是q、k、v三个向量乘乘乘得到的,为什么三个向量乘乘乘就work呢?
q代表query
k代表key
v代表value
将查询和一组键值对映射到输出
scaled dot-product attention
缩放点积注意力机制
query和key的维度一致$d_k$,values的维度是$d_v$
所谓点积,就是$Q \cdot K^T$
所谓缩放,就是在点积后乘上系数$\frac{1}{\sqrt{d_k}}$
然后再对上述结果softmax,因此得到values的权重
然后再将权重乘上values矩阵,得到注意力矩阵
$$
\text{Attention}(Q,K,V)=\text{softmax}(\frac{QK^T}{\sqrt{d_k}})V
$$
在此之前,有两种常见的注意力机制,加性注意力和点积注意力,点积注意力和本文提出的注意力除放缩因素以外没有区别。
两者在理论复杂性上相似,但是在实践中,点积注意力更快速、更节省空间,因为它可以使用高度优化的矩阵乘法代码实现。
在面试的过程中,提到transformer无法绕开的一个八股问题就是上面的注意力机制公式中的QKV代表了什么,这个已经解释过了,还有一个就是为什么要进行放缩即乘上因子$\frac{1}{\sqrt{d_k}}$?
当$d_k$的值较小时,这两种机制的表现相似,但是对于较大的$d_k$值,加性注意力优于不使用缩放的点乘注意力。
在$d_k$也就是keys向量的维度较大时,点积的值会变得很大,那么在反向传播的时候,softmax函数的变化不敏感,导致梯度极小,乘上因子进行缩放可以防止softmax函数在反向传播的时候梯度消失。
the dot products grow large in magnitude
意思是点积幅度变大
这里需要应用到概统的知识,简单来说就是原本的Q、K向量都是归一化过的,但是点积后需要重新归一化,因此乘上因子缩放归一化。
multi-head attention
多头注意力
单通道变多头是怎么个事?
多头注意力机制中将查询、键和值进行h次线性投影,分别投影到不同的、经过学习的线性投影到dk、dk和dv维度上是有益的。
感觉很像CNN中的原始3 channels变成多channels,各个投影版本并行执行注意力函数
$$
\mathrm{MultiHead}(Q,K,V)=\mathrm{Concat}(\mathrm{head}{1},…,\mathrm{head}{\mathrm{h}})W^{O}
$$
$$
\mathrm{where~head_{i}}=\mathrm{Attention}(QW_{i}^{Q},KW_{i}^{K},VW_{i}^{V})
$$
多头注意力允许模型同时关注不同表示子空间在不同位置的信息。使用单个注意力头,平均会抑制这一点。
注意力机制在transformer中的应用
都说attention是transformer的灵魂,那么注意力到底在哪应用了呢?
编码器-解码器注意力层
Q来自前一个解码层
存储的K、V来自编码层的输出
上述操作使得解码器中的每个位置都可以关注输入序列中的所有位置
模仿了S2S模型中的典型编码器-解码器注意力机制
编码器包含了自注意力层
所有K、Q、V来自同一个空间,即编码器的前一层输出
使得解码器中的每个位置都可以处理编码器前一层中的所有位置
解码器中的自注意力层使得解码器中的每个位置都可以关注到该位置之前的所有位置,需要阻止解码器中的左向信息流,保持其自回归的属性
在缩放点积注意力中实现,通过mask out非法位置的所有输入($- \infin$)
position-wise feed-forward networks
这个挺熟悉了,就是过两轮线性全连接层,然后中间夹一个ReLU
虽然线性变换在不同位置是相同的,但它们在层与层之间使用不同的参数。
也类似于用kernel size为1的卷积核进行了两次卷积操作
embeddings and softmax
使用了已学习的embeddings以将输入和输出token转化成$d_{model}$维的输入模型向量
使用了常见的已学习的线性变化和softmax函数以将解码器输出转化成预测下一token的概率
transformer中两个embedding层、预先softmax的线性变化层的权重共享
在embedding层,权重需要乘上系数$\sqrt{d_{model}}$
positional encoding
由于没有循环(递归)或者卷积,为了能够利用序列的顺序关系,需要向模型注入一些序列tokens中相对或者绝对位置信息。
因此在编码器和解码器的底部即输入embeddings中加入位置编码
位置编码的维度也是$d_{model}$,以便于相加
使用了不同频率的正弦和余弦函数作为位置编码
$$
PE_{(pos,2i)}=sin(pos/10000^{2i/d_{\mathrm{model}}})
$$
$$
PE_{(pos,2i+1)}=cos(pos/10000^{2i/d_{\mathrm{model}}})
$$
位置编码的每个维度对应一个正弦波,其波长是一个从$2\pi-10000 \cdot 2\pi$
选择这种编码的原因是让模型容易地学会通过相对位置进行关注
使用正弦版本能够使模型推理时如遇到更长的序列可以进行合理外推。
为什么用Self-Attention
self-attention与循环层、卷积层进行对比。
使用self-attention大致有三个原因
total computational complexity per layer
the amount of computation that can be parallelized
the path length between lond-range dependencies in the network
学习长程依赖是许多序列转化任务中面临的关键挑战
影响学习长程依赖关系能力的一个关键因素是前向和后向信号在网络中必须穿越的路径长度,输入、输出序列任意位置之间的路径越短,学习长距离依赖越容易
不同层组成的复杂度、序列操作复杂度、最长路径长度

可以看到自注意力的操作和最长路径长度都是$O(1)$规模的
训练阶段
看文献学英语
solely:仅仅 可以替换only
**… have become an integral part of ….**:…已经成为…不可或缺的一部分
in all but a few cases:在绝大多数情况下
in conjunction with:与…结合
to the best of our knowledge:据我们所知
be identical to:…与…一样
to this end:因此



